![[Prev]](p_prev.gif)
![[Next]](p_next.gif)
4.3. Simulation von Massenspektren mit MASSIMO
Hat man, wie in Kapitel 4.2 beschrieben, die Wissensbasis, also die Fragmentierungsregeln mit ihren Bewertungsfunktionen, erstellt, können mit dem Programm MASSIMO für beliebige Strukturen die Massenspektren vorhergesagt
werden. Die Beliebigkeit der Strukturen gilt natürlich nur insoweit, als die Gültigkeit der Regeln nicht überschritten wird, die von den Fragmentierungstypen und Molekülen zusammen mit ihren Massenspektren abhängt, die zur Ableitung
der Wissensbasis verwendet wurden. MASSIMO wendet, beginnend mit der Ausgangsverbindung, zunächst die zwei Ionisationstypen (n- und 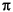 -Ionisation) und dann die in der Wissensbasis kodierten Fragmentierungstypen auf alle entstehenden
Produktkationen an. Für alle Reaktionen wird die Reaktionswahrscheinlichkeit und daraus für alle konkurrierenden Reaktionen die Stoffmenge der beteiligten Ionen berechnet. Dies wird solange fortgesetzt, bis entweder die Masse oder die Stoffmenge des
Produkts unter einen bestimmten Schwellwert fällt.
-Ionisation) und dann die in der Wissensbasis kodierten Fragmentierungstypen auf alle entstehenden
Produktkationen an. Für alle Reaktionen wird die Reaktionswahrscheinlichkeit und daraus für alle konkurrierenden Reaktionen die Stoffmenge der beteiligten Ionen berechnet. Dies wird solange fortgesetzt, bis entweder die Masse oder die Stoffmenge des
Produkts unter einen bestimmten Schwellwert fällt.
4.3.1. Verwendete Regeln
Als Regeln wurden neben den beiden Ionisationsarten (n- und 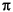 -) die vier Fragmentierungstypen verwendet, für die in Kapitel 4.2.5.2 eine Bewertungsfunktion oder eine neuronales Netz abgeleitet wurde.
Sie sind in Abbildung 32 gezeigt.
-) die vier Fragmentierungstypen verwendet, für die in Kapitel 4.2.5.2 eine Bewertungsfunktion oder eine neuronales Netz abgeleitet wurde.
Sie sind in Abbildung 32 gezeigt.
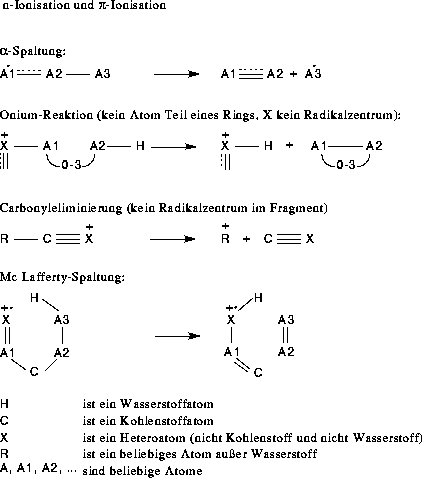
Abbildung 32: Fragmentierungstypen für die Vorhersage von Massenspektren.
So hat man Bewertungen für die vier Fragmentierungstypen  -Spaltung, Oniumreaktion, Carbonyleliminierung und McLafferty-Spaltung. Aber bevor die Fragmentierungen zum Zuge kommen, muß das Molekül ionisiert werden. Die
Regeln für die beiden Ionisationsarten konnten aus dem Satz von Regeln für FRANZ entnommen werden, aber für die Ableitung der Wahrscheinlichkeitsfunktionen standen keine Daten zur Verfügung, da die verwendeten 103 Moleküle alle nur
eine funktionelle Gruppe und somit meist nur einen Ionisationsort besitzen. Die Verteilung der Stoffmengen auf die unterschiedlichen Ionisationsprodukte wurde daher an die Boltzmann-Verteilung angelehnt. Die Umsätze für die verschiedenen Ionisationen
Ui werden folgendermaßen bestimmt (Die Stoffmenge der nicht ionisierten Verbindung ist ohne Belang, da sie kein Signal zum Massenspektrum beisteuert.):
-Spaltung, Oniumreaktion, Carbonyleliminierung und McLafferty-Spaltung. Aber bevor die Fragmentierungen zum Zuge kommen, muß das Molekül ionisiert werden. Die
Regeln für die beiden Ionisationsarten konnten aus dem Satz von Regeln für FRANZ entnommen werden, aber für die Ableitung der Wahrscheinlichkeitsfunktionen standen keine Daten zur Verfügung, da die verwendeten 103 Moleküle alle nur
eine funktionelle Gruppe und somit meist nur einen Ionisationsort besitzen. Die Verteilung der Stoffmengen auf die unterschiedlichen Ionisationsprodukte wurde daher an die Boltzmann-Verteilung angelehnt. Die Umsätze für die verschiedenen Ionisationen
Ui werden folgendermaßen bestimmt (Die Stoffmenge der nicht ionisierten Verbindung ist ohne Belang, da sie kein Signal zum Massenspektrum beisteuert.):

IP ist dabei das erste Ionisationspotential in Elektronenvolt (eV), das aus den physikochemischen Parametern berechnet wird [26][46]. c ist eine Konstante, die an bifunktionellen
Verbindungen wie 11-Aminododecansäuremethylester zu 2.0 bestimmt wurde. Diese Verbindungen haben zwei Ionisationsorte (ohne 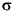 -Ionisation), bei denen die Ionisation an einem Zentrum deutlich dominiert. c wurde so gewählt,
daß die Signalverhältnisse der beiden Signalgruppen für die Ionisationen (m/z 72 für das Produkt der McLafferty-Spaltung und m/z M-1, M-15 sowie m/z 44 für die Produkte der
-Ionisation), bei denen die Ionisation an einem Zentrum deutlich dominiert. c wurde so gewählt,
daß die Signalverhältnisse der beiden Signalgruppen für die Ionisationen (m/z 72 für das Produkt der McLafferty-Spaltung und m/z M-1, M-15 sowie m/z 44 für die Produkte der  -Spaltungen von der ionisierten
Aminogruppe aus) im simulierten Massenspektrum gut wiedergegeben werden (siehe Abbildung 33).
-Spaltungen von der ionisierten
Aminogruppe aus) im simulierten Massenspektrum gut wiedergegeben werden (siehe Abbildung 33).
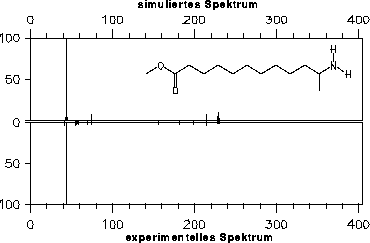
Abbildung 33: Spektrenvergleich für 11-Aminododecansäuremethylester (experimentelles Spektrum [7]).
Für 11-Aminododecansäuremethylester erhält man Ionisationspotentiale von 8.96 eV für die Aminogruppe und 10.23 eV für das freie Elektronenpaar an der Carboxylgruppe. Die verwendete Methode zur Berechnung der Ionisationspotentiale kann
nur das niedrigste Potential einer funktionellen Gruppe berechnen. Die übrigen Ionisationen einer funktionellen Gruppe besitzen mit ihren höheren Ionisationspotentialen deutlich geringere Ionisationswahrscheinlichkeiten und können deshalb vernachlässigt
werden. Aus diesem Grund wird auch für die Carbonylgruppe nur eine Ionisation erzeugt. Nach der Formel 3 ergibt sich dann eine Verteilung von 92.7% Ionisation an der Aminogruppe und nur zu 7.3% an der Carboxylgruppe,
was recht gut mit dem Spektrum in Abbildung 33 vereinbar ist. Das Signal bei m/z 72 (siehe Abbildung 33) ist etwas kleiner als simuliert, da für Signale mit geringer Intensität
im experimentellen Massenspektrum fast immer eine zu geringe Intensität bestimmt wird [8] und bei einer noch stärkeren Gewichtung der Ionisationsumsätze die Gefahr besteht, daß einige Signale überhaupt
nicht mehr im simulierten Spektrum zu sehen sind, wenn das Ionisationspotential etwas zu hoch berechnet wird. Die Genauigkeit der berechneten Ionisationspotentiale ist etwa 0.3 eV, die der experimentell bestimmten ist 0.05 bis 0.2 eV [26].
Simuliert man beispielhaft das Massenspektrum von 3-Hexanon (siehe Abbildung 34) für Carbonylverbindungen, fällt auf, daß die beiden Carbonyleliminierungen (m/z 71 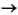 43 und 57
43 und 57  29) nach den
29) nach den  -Spaltungen vom Carbonylsauerstoffatom aus zu hoch bewertet sind. Das Signal bei m/z 72 ist das Produkt der McLafferty-Spaltung. Diese ist auch zu hoch bewertet, da für die wenig reaktiven
McLafferty-Spaltungen der Mittelwert der Reaktionswahrscheinlichkeiten von 0.002 bis 0.544 genommen wurde. 3-Hexanon war im Trainingsdatensatz und hatte eine Wahrscheinlichkeit für die McLafferty-Reaktion von 0.079 (siehe Reaktion 9 im Anhang
D.2.4). Die Signale bei den Massen m/z 41, 39 und 27 können nicht simuliert werden, da der Regelsatz die Wasserstoffmoleküleliminierung nicht enthält, durch die diese Signale aus den Fragmenten der Massen m/z 43 und 29 entstehen.
-Spaltungen vom Carbonylsauerstoffatom aus zu hoch bewertet sind. Das Signal bei m/z 72 ist das Produkt der McLafferty-Spaltung. Diese ist auch zu hoch bewertet, da für die wenig reaktiven
McLafferty-Spaltungen der Mittelwert der Reaktionswahrscheinlichkeiten von 0.002 bis 0.544 genommen wurde. 3-Hexanon war im Trainingsdatensatz und hatte eine Wahrscheinlichkeit für die McLafferty-Reaktion von 0.079 (siehe Reaktion 9 im Anhang
D.2.4). Die Signale bei den Massen m/z 41, 39 und 27 können nicht simuliert werden, da der Regelsatz die Wasserstoffmoleküleliminierung nicht enthält, durch die diese Signale aus den Fragmenten der Massen m/z 43 und 29 entstehen.
Abbildung 34: Spektrenvergleich für 3-Hexanon (experimentelles Spektrum [22]).
Die zu hohe Bewertung der Carbonyleliminierungen liegt daran, daß FRANZ bei der Bestimmung der Wahrscheinlichkeiten offensichtlich weitere zum Edukt der Reaktionen gleich schwere Ionen gefunden hat, die nicht zu einem Umlagerungssystem zusammengefaßt
wurden, da Umlagerungen durch die Wahl der Regeln und Moleküle ausgeschlossen wurden. So wird die Stoffmenge auf die beiden Edukte verteilt und dem Edukt der Carbonyleliminierung möglicherweise eine zu geringe Stoffmenge zugewiesen, wodurch eine zu
hohe Reaktionswahrscheinlichkeit ermittelt wird.
Nimmt man die Hälfte der Reaktionswahrscheinlichkeit, die das neuronale Netz für die Carbonyleliminierung liefert, können die Spektren von Carbonylverbindungen gut simuliert werden, wie auch das Spektrum von 3-Hexanon in Abbildung
35 zeigt.
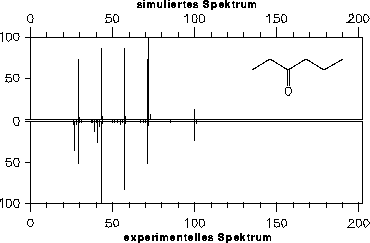
Abbildung 35: Spektrenvergleich für 3-Hexanon mit halber Reaktionswahrscheinlichkeit für die Carbonyleliminierung (experimentelles Spektrum [22]).
Gleiches gilt auch für die Oniumspaltung. Deshalb werden auch die Wahrscheinlichkeiten dieses Netzes für die Verwendung zur Simulation in MASSIMO mit 0.5 multipliziert.
4.3.2. Beispiele für die Leistungsfähigkeit des Ansatzes
Mit den Regeln, wie sie in Kapitel 4.3.1 beschrieben sind, also mit zwei Ionisations- (n und  ) und vier Fragmentierungstypen (
) und vier Fragmentierungstypen ( -Spaltung, Oniumreaktion, Carbonyleliminierung
und McLafferty-Spaltung), soll nun an einigen Beispielen die Simulation von Massenspektren gezeigt werden. Die im experimentellen Spektrum zusätzlich erscheinenden Signale stammen von Fragmentierungstypen, für die eine Vorhersagefunktion für
die Reaktionswahrscheinlichkeit fehlt und deshalb nicht im Satz von Reaktionstypen für die Simulation enthalten sind. Beispiele für die Simulation von Massenspektren mit MASSIMO, bei denen der größte Teil der Summe der Signalintensitäten
vorhergesagt werden kann, sind in den Abschnitten 4.3.2.2 bis 4.3.2.4 gezeigt. Die experimentellen Massenspektren sind den Datenbanken von MassLib [22]
und SpecInfo [7] entnommen und waren mit Ausnahme von Butylmethylpropylamin mit seinem Spektrum (siehe Abbildung 43) nicht im Datensatz enthalten, mit dem die Wahrscheinlichkeitsfunktionen
abgeleitet wurden.
-Spaltung, Oniumreaktion, Carbonyleliminierung
und McLafferty-Spaltung), soll nun an einigen Beispielen die Simulation von Massenspektren gezeigt werden. Die im experimentellen Spektrum zusätzlich erscheinenden Signale stammen von Fragmentierungstypen, für die eine Vorhersagefunktion für
die Reaktionswahrscheinlichkeit fehlt und deshalb nicht im Satz von Reaktionstypen für die Simulation enthalten sind. Beispiele für die Simulation von Massenspektren mit MASSIMO, bei denen der größte Teil der Summe der Signalintensitäten
vorhergesagt werden kann, sind in den Abschnitten 4.3.2.2 bis 4.3.2.4 gezeigt. Die experimentellen Massenspektren sind den Datenbanken von MassLib [22]
und SpecInfo [7] entnommen und waren mit Ausnahme von Butylmethylpropylamin mit seinem Spektrum (siehe Abbildung 43) nicht im Datensatz enthalten, mit dem die Wahrscheinlichkeitsfunktionen
abgeleitet wurden.
4.3.2.1. Vergleich von simulierten und experimentellen Spektren
In den Abbildungen 36 und 37 sind die simulierten gegen die experimentellen Massenspektren von 3-Methoxy-3-methylhexan und N-Ethylbutylamid aufgetragen. Die Intensitäten der Signale
von Fragmenten, die von den eingesetzten Regeln erzeugt werden, können gut vorhergesagt werden. Die nicht simulierten Signale werden von Fragmentierungstypen gebildet, für die keine Vorhersagefunktion für die Reaktionswahrscheinlichkeit vorhanden
ist und deshalb nicht im Satz von Reaktionstypen enthalten ist, der zur Simulation verwendet wurde. In Abbildung 36 sieht man schön die Abstufung der verschiedenen  -Spaltungen ausgehend vom
ionisierten Sauerstoffatom.
-Spaltungen ausgehend vom
ionisierten Sauerstoffatom.
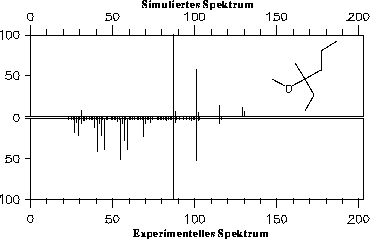
Abbildung 36: Simuliertes Massenspektrum von 3-Methoxy-3-methylhexan.
Obgleich im Trainingssatz neben Carbonsäuren und Estern nur ein nicht N-substituiertes Amid enthalten war, nämlich Hexylamid, werden die Signalintensitäten im Spektrum von N-Ethylbutylamid unter Berücksichtigung der fehlenden Reaktionstypen
gut simuliert (nicht simulierte Signale siehe oben). Die neuronalen Netze für die Bestimmung der Reaktionswahrscheinlichkeiten konnten also verallgemeinern und damit auch Wahrscheinlichkeiten für Reaktionen mit ähnlichen physikochemischen Eigenschaften
am Reaktionszentrum vorhersagen.
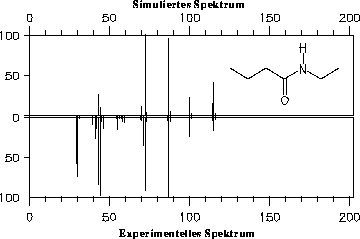
Abbildung 37: Simuliertes Massenspektrum von N-Ethylbutylamid.
Schließlich zeigt Abbildung 38 noch ein Beispiel für eine halogenhaltige, bifunktionelle Verbindung.
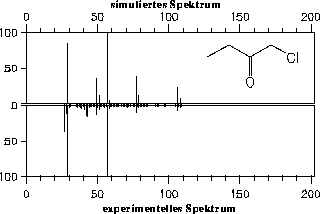
Abbildung 38: Simuliertes Massenspektrum von 1-Chlor-2-butanon.
4.3.2.2. Selektion eines Strukturvorschlages durch Spektrenvergleich
Ist es möglich für verschiedene, in Betracht kommende Verbindungen die Massenspektren zu simulieren, kann durch den Vergleich mit dem experimentellen Spektrum die richtige Struktur herausgefunden werden. Die Güte dieser Selektion ist um so besser,
je besser die simulierten Spektren sind. Haben die Substanzen, aus denen die richtige ausgewählt werden soll, eine unterschiedliche Masse, kann schon über den Molekülpeak eine Entscheidung getroffen werden. Deshalb wurden für dieses Beispiel
drei isomere Verbindungen der Summenformel C6H13NO genommen, für die auf diese einfache Weise nicht zum Ziel gekommen werden kann. Dabei wurden Strukturen ausgewählt, deren experimentelles Massenspektrum zur Verfügung stand. Als einfaches Vergleichsmaß
wird hier das Skalarprodukt verwendet, wobei die Massenspektren als Vektor aufgefaßt werden, dessen Elemente den Massen entsprechen und die Werte den Intensitäten. Ist das Signal bei m/z 57 der Basepeak, hat das 57. Element des Vektors den Wert 1.0
= 100%. Für Massen, die nicht im Spektrum beobachtet werden, ist der Wert null. Abbildung 39 zeigt nun die mit MASSIMO für die drei Strukturen simulierten Spektren und die Skalarprodukte dieser mit dem experimentellen
Spektrum. Das Skalarprodukt hat einen Wertebereich von null bis eins, wobei identische Spektren den Wert eins besitzen. Das Spektrum der richtigen Struktur hat demnach das höchste Skalarprodukt.
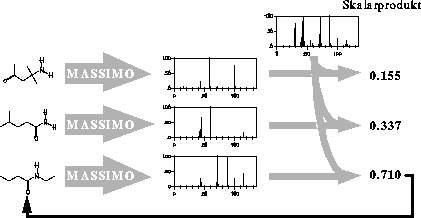
Abbildung 39: Selektion einer aus drei isomeren Verbindungen.
Da für alle drei Verbindungen das experimentelle Massenspektrum vorhanden war, wurde dieser Vergleich auch für die anderen zwei experimentellen Spektren durchgeführt. Alle drei Vergleiche sind in Abbildung 40
zusammengefaßt. Eine Spalte entspricht dabei einer Selektion, deren letzte die Selektion in Abbildung 39 ist.
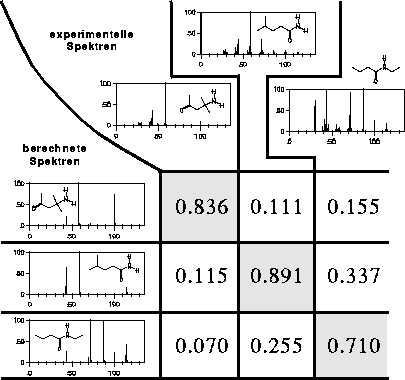
Abbildung 40: Vergleich aller drei Selektionen.
Vergleicht man diese drei Selektionen (Spalten) miteinander, stellt man fest, daß die anderen beiden Entscheidungen noch sicherer getroffen werden, da das Skalarprodukt für den Spektrenvergleich der richtigen Struktur noch größer und das
mit dem nächstkleineren Wert noch kleiner ist. Die Felder für die richtigen Strukturen sind grau unterlegt.
4.3.2.3. Auffinden falscher Spektren in Datenbanken
Im Rahmen der Überprüfung, für welche Substanzen gute Massenspektren simuliert werden können, wurde auch das Spektrum von 11-Aminotridecansäuremethylester vorhergesagt und mit dem experimentellen aus der Datenbank (SpecInfo [7])
verglichen. Diese beiden Spektren sind in Abbildung 41 zu sehen.
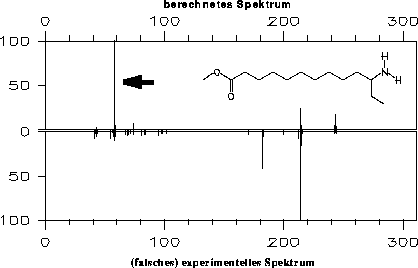
Abbildung 41: Spektrenvergleich von 11-Aminotridecansäuremethylester.
Beim Vergleich fällt auf, daß der Basepeak im vorhergesagten Spektrum bei m/z 58 (mit einem Pfeil markiert) im experimentellen Spektrum lediglich durch ein Signal von etwa 10% vertreten ist. Ähnlich verhält es sich in umgekehrter Weise mit
dem Basepeak im experimentellen Spektrum. Betrachtet man auch den restlichen Teil der Spektren, kommt man zur Überzeugung, daß entweder das simulierte Spektrum falsch oder die beiden Spektren nicht zur selben Struktur gehören.
Bedenkt man, daß in Datenbanken oft auch ältere Spektren enthalten sind, bei denen die Zuordnung der Struktur durch die geringeren analytischen Möglichkeiten nicht mit der heute üblichen Sicherheit erfolgen konnte, muß man bei solchen
Spektren durchaus mit der Angabe einer falschen Struktur rechnen. Darüber hinaus wurden viele dieser Spektren aus der Literatur abgetippt, was nicht in allen Fällen fehlerfrei gemacht wurde. Zudem wurden in der Literatur oft Signale mit geringer Intensität
weggelassen. [8] Ausgehend von der angegebenen Struktur müßte allerdings der Peak bei m/z 58 ( -Spaltung von der Aminogruppe) die größte Intensität besitzen, was auch
vom Massenspektroskopieexperten bestätigt wurde [8]. Auf diese Weise wurde also eine falsche Spektrum-Struktur-Zuordnung in einer Datenbank aufgefunden.
-Spaltung von der Aminogruppe) die größte Intensität besitzen, was auch
vom Massenspektroskopieexperten bestätigt wurde [8]. Auf diese Weise wurde also eine falsche Spektrum-Struktur-Zuordnung in einer Datenbank aufgefunden.
Mit einem Regelsatz, der für die Simulation nahezu aller organischer Verbindungen eingesetzt werden kann, könnte man den Inhalt von Datenbanken automatisch überprüfen. Die aussortierten Spektren sollten danach noch von einem Experten getestet
werden, ob diese Entscheidung richtig war und es sich nicht doch um ein korrektes Spektrum handelt. Im Vergleich dazu müßten Experten ohne ein solches Hilfsmittel jedes in der Datenbank enthaltene Spektrum kontrollieren.
In gleicher Weise wurde die Fehlzuordnung für 1,1-Dimethoxyhexadecan (experimentelles Spektrum [7]) aufgedeckt. In diesem Fall konnte auch noch der Grund für die falsche Struktur angegeben werden. Bei der Aufnahme
des Spektrums wurde die Verbindung 1,1-Dimethoxyhexadecan in das Inlett des Massenspektrometers geleitet, dort aber so stark erhitzt, daß die Verbindung Methanol eliminiert hat, und so das Spektrum des Pyrolyseprodukts 1-Methoxyhexadec-1-en aufgenommen
wurde. [47] Dies wird auch von den von MASSIMO simulierten Spektren bestätigt (siehe Abbildung 42).
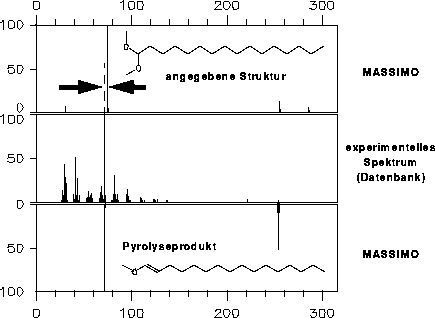
Abbildung 42: Statt von 1,1-Dimethoxyhexadecan wurde das Spektrum vom Pyrolyseprodukt 1-Methoxyhexadec-1-en aufgenommen.
4.3.2.4. Unterstützung von Massenspektroskopieexperten durch die Simulation von Spektren
Eine weitere Einsatzmöglichkeit der Spektrensimulation ist die Unterstützung des Massenspektroskopieexperten. Dies erfolgt zunächst, wie es in Kapitel 4.3.2.2 beschrieben wurde. Ist die Struktur dann aufgeklärt,
muß vom Experten das Massenspektrum aufgrund dieser Struktur verifiziert werden. MASSIMO kann dabei dem Massenspektroskopieexperten zur Seite stehen und seinen Arbeitsaufwand reduzieren. Simuliert MASSIMO den größten Teil der Signale im Spektrum,
wobei der Weg der Fragmentierungen zu den entsprechenden Ionen angegeben wird, gehören diese Signale zur bestimmten Struktur und der Experte muß sich nur noch um die wenigen Signale kümmern, die von MASSIMO nicht vorhergesagt werden. Abbildung
43 zeigt das simulierte und das experimentelle Spektrum von Butylmethylpropylamin.

Abbildung 43: Spektrenvergleich von Butylmethylpropylamin.
Vier der fünf intensiven Signale werden von MASSIMO simuliert. Die Aufgabe des Experten hat sich auf die Erklärung des letzten Peaks bei m/z 58 reduziert. Das dazugehörige Fragment wird über die pericyclische Reaktion in Abbildung
44 aus den  -Spaltungsprodukten des Amins gebildet [18].
-Spaltungsprodukten des Amins gebildet [18].

Abbildung 44: Pericyclische Reaktion zur Bildung des Fragments m/z 58.
Sagt MASSMO ein Signal vorher, das nicht im experimentellen Spektrum zu sehen ist, ist zu überlegen, warum die Reaktion zur Bildung dieses Fragments für die angegebene Struktur nicht stattfindet bzw. ob es sich wirklich um die richtige Struktur handelt.
Butylmethylpropylamin ist ein Beispiel, bei dem dies auch mit der beschränkten Einsatzfähigkeit der verwendeten Regeln erfolgreich gezeigt werden kann. Es ist im Trainingssatz zur Ableitung der Wahrscheinlichkeitsfunktionen enthalten gewesen. Für
einen breiteren Einsatz müßten allerdings die Regeln für MASSIMO noch verbessert werden.
4.3.3. Erweiterung der Regeln um die Wasserstoffumlagerung
Bisher wurden Umlagerungsreaktionen und damit speziell alle Umlagerungsreaktionstypen wie die Wasserstoffumlagerung vermieden, da sie FRANZ bei der Bestimmung der Reaktionswahrscheinlichkeiten so große Probleme machen (siehe 4.2.2.3),
daß mit den so gewonnenen Daten keine erfolgversprechenden Simulationen erwartet werden können. Es soll nun versucht werden, die Wasserstoffumlagerung nachträglich zum Satz der Fragmentierungstypen hinzuzufügen.
4.3.3.1. Erstellung der Regel für die Wasserstoffumlagerung
MASSIMO hat eine besondere Behandlung für Umlagerungsreaktionstypen, wie die Wasserstoffumlagerung. Für solche Reaktionen werden dann die Gleichgewichtskonstanten statt der Geschwindigkeitskonstante angegeben. Bevor MASSIMO von einem Kation die Fragmentierungen
ausführt, werden alle Reaktionen von Umlagerungsreaktionstypen erzeugt, wobei dies auch für alle dabei entstehenden Produkte solange fortgesetzt wird, bis keine neuen Umlagerungsreaktionen mehr gefunden werden. Ist das Umlagerungsprodukt schon im
Umlagerungssystem enthalten, wird die Reaktion verworfen, um das Umlagerungssystem mit seinen Gleichgewichtskonstanten eindeutig lösbar zu halten. Dahinter steht die Annahme, daß der zuerst gefundene, kürzeste Weg auch den größten Umsatz
hat. Für alle weiteren Reaktionen, die ein Umlagerungsprodukt bilden, wird angenommen, daß sie nur einen geringen Beitrag zur Bildung beitragen, und werden vernachlässigt. Für die Bestimmung der Stoffmengen der Umlagerungsprodukte wird angenommen,
daß alle Umlagerungen genügend Zeit haben, sich auch einzustellen. Dies ist zwar in der Realität nicht ganz gegeben. Es soll hier untersucht werden, wie gut es mit diesem einfachen Ansatz dennoch möglich ist, die Signale zu simulieren, deren
Ionen über Wasserstoffumlagerungen gebildet werden. Bei langkettigen Carbonsäuren und Estern sieht man die Signale der Produkte der  -Spaltungen, die von den Produkten der Wasserstoffumlagerungen ausgehen. Diese wiederum
werden aus der am Carbonylsauerstoffatom ionisierten Carbonsäure bzw. Ester gebildet. Abbildung 45 zeigt zunächst das simulierte Spektrum ohne die Wassersoffumlagerung.
-Spaltungen, die von den Produkten der Wasserstoffumlagerungen ausgehen. Diese wiederum
werden aus der am Carbonylsauerstoffatom ionisierten Carbonsäure bzw. Ester gebildet. Abbildung 45 zeigt zunächst das simulierte Spektrum ohne die Wassersoffumlagerung.
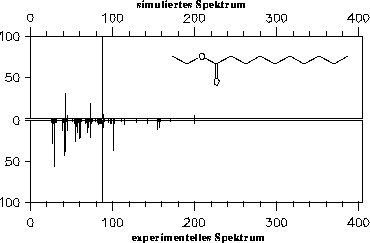
Abbildung 45: Simuliertes Massenspektrum für Decansäureethylester ohne Wasserstoffumlagerung (experimentelles Spektrum [22]).
Die Wasserstoffumlagerungen wurden dem erweiterten Regelsatz aus Kapitel 4.2.3.1 entnommen und auf die Kettenlängen von zwei bis vier beschränkt. Es wurden also Wasserstoffumlagerungen über 5-, 6- und 7-gliedrige,
ringförmige Übergangszustände zugelassen. Die Reaktionstypen sind in Abbildung 46 gezeigt.
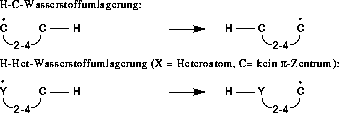
Abbildung 46: Wasserstoffumlagerungen.
Desweiteren wurden Wasserstoffumlagerungen auf ein Kohlenstoffradikal ausgeschlossen, wenn dieses mit einer positiven Ladung konjugiert ist, und mehrfache Wasserstoffumlagerungen auf eine funktionelle Gruppe wurden, wie in 4.2.2.4
beschrieben, unterdrückt. Die Gleichgewichtskonstante für Umlagerung auf ein Kohlenstoffatom wurde aufgrund von simulierten Testspektren auf 0.3 und die auf Heteroatome auf 0.03 gesetzt. Ansonsten wurden die Regeln inklusive der Bewertungen aus Kapitel
4.3.1 übernommen. Da das neuronale Netz zur Bewertung der  -Spaltungen nicht für Spaltungen nach Wasserstoffumlagerungen trainiert wurde und es in diesen Fällen für die Abspaltung
von Wasserstoffradikalen viel zu hohe Wahrscheinlichkeiten liefert, wurde für diese Reaktionen die Wahrscheinlichkeit auf 6% der vom Netz gelieferten Wahrscheinlichkeit herabgesetzt. Mit den so erstellten Regeln erhält man das in Abbildung
47 gezeigte simulierte Spektrum.
-Spaltungen nicht für Spaltungen nach Wasserstoffumlagerungen trainiert wurde und es in diesen Fällen für die Abspaltung
von Wasserstoffradikalen viel zu hohe Wahrscheinlichkeiten liefert, wurde für diese Reaktionen die Wahrscheinlichkeit auf 6% der vom Netz gelieferten Wahrscheinlichkeit herabgesetzt. Mit den so erstellten Regeln erhält man das in Abbildung
47 gezeigte simulierte Spektrum.
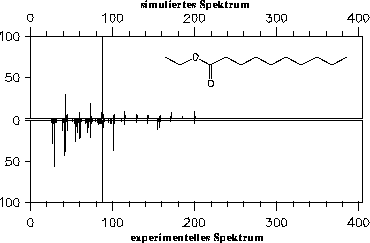
Abbildung 47: Simuliertes Spektrum von Decansäureethylester mit Wasserstoffumlagerung.
Bei näherer Betrachtung des simulierten Spektrums mit Wasserstoffumlagerung kann man vermuten, daß es so möglich sein könnte, die Signale der Produkte der  -Spaltungen nach einer Wasserstoffumlagerung vorherzusagen.
An den Intensitäten sind aber noch Verbesserungen nötig und auch die Signale bei einer Masseneinheit höher, die von den
-Spaltungen nach einer Wasserstoffumlagerung vorherzusagen.
An den Intensitäten sind aber noch Verbesserungen nötig und auch die Signale bei einer Masseneinheit höher, die von den  -Spaltungen in die andere Richtung stammen und im Massenspektrometer nicht vorkommen, müßten
ausgeschlossen werden. Für eine Ähnlichkeitssuche, für die dieses Experiment durchgeführt wurde, könnte das simulierte Spektrum möglicherweise dennoch ausreichen.
-Spaltungen in die andere Richtung stammen und im Massenspektrometer nicht vorkommen, müßten
ausgeschlossen werden. Für eine Ähnlichkeitssuche, für die dieses Experiment durchgeführt wurde, könnte das simulierte Spektrum möglicherweise dennoch ausreichen.
Gewichtet man die verschiedenen Wasserstoffumlagerungen so, wie sie in Kapitel 4.2.2.3 für Fettsäuren und deren Ester als geeignet vorgestellt wurden, und schließt die  -Spaltungen
in die falsche Richtung aus, kann das simulierte Spektrum verbessert werden.
-Spaltungen
in die falsche Richtung aus, kann das simulierte Spektrum verbessert werden.
Dazu wurden die  -Spaltungen ausgeschlossen, bei denen kein Radikal als Neutralfragment abgespalten wird, wodurch die
-Spaltungen ausgeschlossen, bei denen kein Radikal als Neutralfragment abgespalten wird, wodurch die  -Spaltungen in die falsche Richtung verhindert werden. Die Gleichgewichtskonstanten der
Wasserstoffumlagerung auf ein Kohlenstoffatom wurden für 5-gliedrige Übergangszustände auf 0.16, für 6-gliedrige auf 0.35 und für 7-gliedrige auf 0.08 gesetzt. Für die Wasserstoffumlagerung auf ein Heteroatom wurde nur eine 1,3-Wasserstoffverschiebung
erlaubt, die sicher als zwei 1,2-Verschiebungen entlang des
-Spaltungen in die falsche Richtung verhindert werden. Die Gleichgewichtskonstanten der
Wasserstoffumlagerung auf ein Kohlenstoffatom wurden für 5-gliedrige Übergangszustände auf 0.16, für 6-gliedrige auf 0.35 und für 7-gliedrige auf 0.08 gesetzt. Für die Wasserstoffumlagerung auf ein Heteroatom wurde nur eine 1,3-Wasserstoffverschiebung
erlaubt, die sicher als zwei 1,2-Verschiebungen entlang des 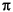 -Systems der Säure oder des Esters stattfindet. Die Gleichgewichtskonstante wurde abhängig von der Größe des Kations so bestimmt, daß sich für
Decansäureethylester (38 Atome) ein Wert von 0.08 ergibt und für Methylstearat (59 Atome) 0.28. Das Spektrum von Decansäureethylester ist in Abbildung 48 gezeigt.
-Systems der Säure oder des Esters stattfindet. Die Gleichgewichtskonstante wurde abhängig von der Größe des Kations so bestimmt, daß sich für
Decansäureethylester (38 Atome) ein Wert von 0.08 ergibt und für Methylstearat (59 Atome) 0.28. Das Spektrum von Decansäureethylester ist in Abbildung 48 gezeigt.
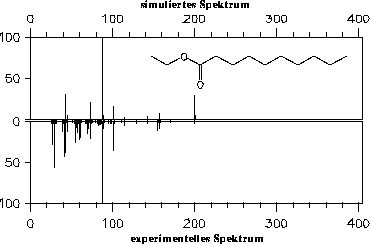
Abbildung 48: Simuliertes Spektrum von Decansäureethylester mit gewichteter Wasserstoffumlagerung.
Angeglichen wurden die Werte der Gleichgewichtskonstanten für die Wasserstoffumlagerung an Methylstearat, dessen Spektrum in Abbildung 49 gezeigt ist und gut mit dem experimentellen übereinstimmt. An Methylstearat
wurde in Kapitel 4.2.2.3 die Güte der Gewichtung der verschiedenen, ringförmigen Übergangszustände gezeigt, an die die Gleichgewichtskonstanten angepaßt wurden (siehe Abbildung
10 auf Seite 21).
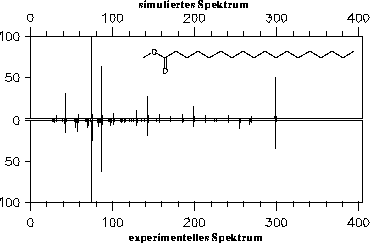
Abbildung 49: Simuliertes Spektrum von Methylstearat mit gewichteter Wasserstoffumlagerung.
Die so simulierten Spektren können sicherlich für die Suche in einer Spektrendatenbank verwendet werden.
4.3.3.2. Andere Quellen für die Wahrscheinlichkeiten der Umlagerungen
Eine Überlegung, an die Geschwindigkeitskonstanten der Wasserstoffumlagerungen zu kommen, war, diese aus semiempirisch berechneten Enthalpien und Entropien zu bestimmen. Für die Aktivierungsenergie der Wasserstoffumlagerung sind Werte in der Literatur
[48] zu finden. Die Werte sind allerdings immer nur für das einfachste der möglichen Radikale angegeben. Um überprüfen zu können, ob die Werte auch für die im Massenspektrometer auftretenden
Radikalkationen gelten, wurde zunächst getestet, ob die Ergebnisse reproduziert werden können. Für die Wasserstoffumlagerung über einen 6-gliedrigen Übergangszustand für das 2-Heptylradikal wird in [48]
ein Wert von 21.99 kcal/mol angegeben. In Abbildung 50 sind die Ergebnisse für die Radikale 2-Heptyl-, 3-Nonyl- und 4-Undecylradikal für diese Umlagerung angegeben. Für das Heptylradikal ergibt sich eine Aktivierungsenergie
von 21.13 kcal/mol gegenüber 21.99 kcal/mol aus [48], also keine allzu große Differenz. Für die anderen beiden Radikale ist die Aktivierungsenergie durch die bessere Stabilisierung der längeren Alkylketten
um 1.17 kcal/mol niedriger. Alle Werte wurden mit der Methode AM1 [49] in VAMP5 [50] bestimmt.

Abbildung 50: Mit AM1 bestimmte Aktivierungsenergien für die 1,5-Wasserstoffumlagerung für das 2-Heptyl-, 3-Nonyl- und 4-Undecylradikal.
Geht man nun zu einem Radikalkation über, das im Massenspektrometer von Tridecansäuremethylester auftritt, über, ist es nicht mehr möglich, den Übergangszustand sauber zu berechnen, da für die optimierte Struktur zwei statt einer
negativen Eigenfrequenz berechnet werden. Die zweite Eigenfrequenz ist mit -5.82 cm-1 nahe null, läßt sich aber nicht ganz vermeiden. Die Strukturen und Werte sind in Abbildung 51 gezeigt.
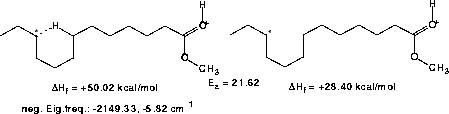
Abbildung 51: AM1-Berechnungen für das am Carbonylsauerstoffatom protonierte 11-Tridecansäuremethylesterradikal.
Die zweite negative Eigenfrequenz liegt an der protonierten Estergruppe, wie die Berechnungen am protonierten Pentansäuremethylester in Abbildung 52 für beide möglichen Orientierungen des Protons zeigen.
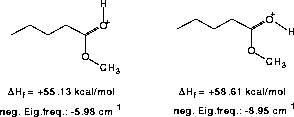
Abbildung 52: AM1-Rechnungen des protonierten Pentansäuremethylesters.
Da die Berechnungen für die tatsächlich im Massenspektrometer auftretenden Ionen nicht verifiziert werden konnten, obgleich die ermittelten Werte höchstwahrscheinlich doch zutreffend sind, sowie in der Literatur die Werte für 7- und 8-gliedrige
Ringe als Übergangszustände nicht enthalten waren, wurden die Bestrebungen eingestellt, die Wahrscheinlichkeiten für die Wasserstoffumlagerungen semiempirisch zu bestimmen. Eine Berechnung der fehlenden Werte sowie der Entropien wäre wegen
der großen Zahl der Freiheitsgrade für diese Radikale sehr zeitaufwendig gewesen und hätte nicht notwendigerweise brauchbare Ergebnisse geliefert.
![[Prev]](p_prev.gif)
![[Next]](p_next.gif)
robert(at)robert-hoellering.de
Copyright © 1998, Höllering Universität Erlangen-Nürnberg. All rights
reserved.
![[Prev]](p_prev.gif)
![[Next]](p_next.gif)
![[Prev]](p_prev.gif)
![[Next]](p_next.gif)
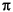 -Ionisation) und dann die in der Wissensbasis kodierten Fragmentierungstypen auf alle entstehenden
Produktkationen an. Für alle Reaktionen wird die Reaktionswahrscheinlichkeit und daraus für alle konkurrierenden Reaktionen die Stoffmenge der beteiligten Ionen berechnet. Dies wird solange fortgesetzt, bis entweder die Masse oder die Stoffmenge des
Produkts unter einen bestimmten Schwellwert fällt.
-Ionisation) und dann die in der Wissensbasis kodierten Fragmentierungstypen auf alle entstehenden
Produktkationen an. Für alle Reaktionen wird die Reaktionswahrscheinlichkeit und daraus für alle konkurrierenden Reaktionen die Stoffmenge der beteiligten Ionen berechnet. Dies wird solange fortgesetzt, bis entweder die Masse oder die Stoffmenge des
Produkts unter einen bestimmten Schwellwert fällt. 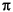 -) die vier Fragmentierungstypen verwendet, für die in Kapitel 4.2.5.2 eine Bewertungsfunktion oder eine neuronales Netz abgeleitet wurde.
Sie sind in Abbildung 32 gezeigt.
-) die vier Fragmentierungstypen verwendet, für die in Kapitel 4.2.5.2 eine Bewertungsfunktion oder eine neuronales Netz abgeleitet wurde.
Sie sind in Abbildung 32 gezeigt.
 -Spaltung, Oniumreaktion, Carbonyleliminierung und McLafferty-Spaltung. Aber bevor die Fragmentierungen zum Zuge kommen, muß das Molekül ionisiert werden. Die
Regeln für die beiden Ionisationsarten konnten aus dem Satz von Regeln für FRANZ entnommen werden, aber für die Ableitung der Wahrscheinlichkeitsfunktionen standen keine Daten zur Verfügung, da die verwendeten 103 Moleküle alle nur
eine funktionelle Gruppe und somit meist nur einen Ionisationsort besitzen. Die Verteilung der Stoffmengen auf die unterschiedlichen Ionisationsprodukte wurde daher an die Boltzmann-Verteilung angelehnt. Die Umsätze für die verschiedenen Ionisationen
Ui werden folgendermaßen bestimmt (Die Stoffmenge der nicht ionisierten Verbindung ist ohne Belang, da sie kein Signal zum Massenspektrum beisteuert.):
-Spaltung, Oniumreaktion, Carbonyleliminierung und McLafferty-Spaltung. Aber bevor die Fragmentierungen zum Zuge kommen, muß das Molekül ionisiert werden. Die
Regeln für die beiden Ionisationsarten konnten aus dem Satz von Regeln für FRANZ entnommen werden, aber für die Ableitung der Wahrscheinlichkeitsfunktionen standen keine Daten zur Verfügung, da die verwendeten 103 Moleküle alle nur
eine funktionelle Gruppe und somit meist nur einen Ionisationsort besitzen. Die Verteilung der Stoffmengen auf die unterschiedlichen Ionisationsprodukte wurde daher an die Boltzmann-Verteilung angelehnt. Die Umsätze für die verschiedenen Ionisationen
Ui werden folgendermaßen bestimmt (Die Stoffmenge der nicht ionisierten Verbindung ist ohne Belang, da sie kein Signal zum Massenspektrum beisteuert.):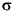 -Ionisation), bei denen die Ionisation an einem Zentrum deutlich dominiert. c wurde so gewählt,
daß die Signalverhältnisse der beiden Signalgruppen für die Ionisationen (m/z 72 für das Produkt der McLafferty-Spaltung und m/z M-1, M-15 sowie m/z 44 für die Produkte der
-Ionisation), bei denen die Ionisation an einem Zentrum deutlich dominiert. c wurde so gewählt,
daß die Signalverhältnisse der beiden Signalgruppen für die Ionisationen (m/z 72 für das Produkt der McLafferty-Spaltung und m/z M-1, M-15 sowie m/z 44 für die Produkte der  -Spaltungen von der ionisierten
Aminogruppe aus) im simulierten Massenspektrum gut wiedergegeben werden (siehe Abbildung 33).
-Spaltungen von der ionisierten
Aminogruppe aus) im simulierten Massenspektrum gut wiedergegeben werden (siehe Abbildung 33).
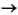 43 und 57
43 und 57 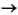 29) nach den
29) nach den  -Spaltungen vom Carbonylsauerstoffatom aus zu hoch bewertet sind. Das Signal bei m/z 72 ist das Produkt der McLafferty-Spaltung. Diese ist auch zu hoch bewertet, da für die wenig reaktiven
McLafferty-Spaltungen der Mittelwert der Reaktionswahrscheinlichkeiten von 0.002 bis 0.544 genommen wurde. 3-Hexanon war im Trainingsdatensatz und hatte eine Wahrscheinlichkeit für die McLafferty-Reaktion von 0.079 (siehe Reaktion 9 im Anhang
D.2.4). Die Signale bei den Massen m/z 41, 39 und 27 können nicht simuliert werden, da der Regelsatz die Wasserstoffmoleküleliminierung nicht enthält, durch die diese Signale aus den Fragmenten der Massen m/z 43 und 29 entstehen.
-Spaltungen vom Carbonylsauerstoffatom aus zu hoch bewertet sind. Das Signal bei m/z 72 ist das Produkt der McLafferty-Spaltung. Diese ist auch zu hoch bewertet, da für die wenig reaktiven
McLafferty-Spaltungen der Mittelwert der Reaktionswahrscheinlichkeiten von 0.002 bis 0.544 genommen wurde. 3-Hexanon war im Trainingsdatensatz und hatte eine Wahrscheinlichkeit für die McLafferty-Reaktion von 0.079 (siehe Reaktion 9 im Anhang
D.2.4). Die Signale bei den Massen m/z 41, 39 und 27 können nicht simuliert werden, da der Regelsatz die Wasserstoffmoleküleliminierung nicht enthält, durch die diese Signale aus den Fragmenten der Massen m/z 43 und 29 entstehen.

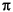 ) und vier Fragmentierungstypen (
) und vier Fragmentierungstypen ( -Spaltung, Oniumreaktion, Carbonyleliminierung
und McLafferty-Spaltung), soll nun an einigen Beispielen die Simulation von Massenspektren gezeigt werden. Die im experimentellen Spektrum zusätzlich erscheinenden Signale stammen von Fragmentierungstypen, für die eine Vorhersagefunktion für
die Reaktionswahrscheinlichkeit fehlt und deshalb nicht im Satz von Reaktionstypen für die Simulation enthalten sind. Beispiele für die Simulation von Massenspektren mit MASSIMO, bei denen der größte Teil der Summe der Signalintensitäten
vorhergesagt werden kann, sind in den Abschnitten 4.3.2.2 bis 4.3.2.4 gezeigt. Die experimentellen Massenspektren sind den Datenbanken von MassLib [22]
und SpecInfo [7] entnommen und waren mit Ausnahme von Butylmethylpropylamin mit seinem Spektrum (siehe Abbildung 43) nicht im Datensatz enthalten, mit dem die Wahrscheinlichkeitsfunktionen
abgeleitet wurden.
-Spaltung, Oniumreaktion, Carbonyleliminierung
und McLafferty-Spaltung), soll nun an einigen Beispielen die Simulation von Massenspektren gezeigt werden. Die im experimentellen Spektrum zusätzlich erscheinenden Signale stammen von Fragmentierungstypen, für die eine Vorhersagefunktion für
die Reaktionswahrscheinlichkeit fehlt und deshalb nicht im Satz von Reaktionstypen für die Simulation enthalten sind. Beispiele für die Simulation von Massenspektren mit MASSIMO, bei denen der größte Teil der Summe der Signalintensitäten
vorhergesagt werden kann, sind in den Abschnitten 4.3.2.2 bis 4.3.2.4 gezeigt. Die experimentellen Massenspektren sind den Datenbanken von MassLib [22]
und SpecInfo [7] entnommen und waren mit Ausnahme von Butylmethylpropylamin mit seinem Spektrum (siehe Abbildung 43) nicht im Datensatz enthalten, mit dem die Wahrscheinlichkeitsfunktionen
abgeleitet wurden.  -Spaltungen ausgehend vom
ionisierten Sauerstoffatom.
-Spaltungen ausgehend vom
ionisierten Sauerstoffatom. 





 -Spaltung von der Aminogruppe) die größte Intensität besitzen, was auch
vom Massenspektroskopieexperten bestätigt wurde [8]. Auf diese Weise wurde also eine falsche Spektrum-Struktur-Zuordnung in einer Datenbank aufgefunden.
-Spaltung von der Aminogruppe) die größte Intensität besitzen, was auch
vom Massenspektroskopieexperten bestätigt wurde [8]. Auf diese Weise wurde also eine falsche Spektrum-Struktur-Zuordnung in einer Datenbank aufgefunden. 

 -Spaltungsprodukten des Amins gebildet [18].
-Spaltungsprodukten des Amins gebildet [18]. 
 -Spaltungen, die von den Produkten der Wasserstoffumlagerungen ausgehen. Diese wiederum
werden aus der am Carbonylsauerstoffatom ionisierten Carbonsäure bzw. Ester gebildet. Abbildung 45 zeigt zunächst das simulierte Spektrum ohne die Wassersoffumlagerung.
-Spaltungen, die von den Produkten der Wasserstoffumlagerungen ausgehen. Diese wiederum
werden aus der am Carbonylsauerstoffatom ionisierten Carbonsäure bzw. Ester gebildet. Abbildung 45 zeigt zunächst das simulierte Spektrum ohne die Wassersoffumlagerung.

 -Spaltungen nicht für Spaltungen nach Wasserstoffumlagerungen trainiert wurde und es in diesen Fällen für die Abspaltung
von Wasserstoffradikalen viel zu hohe Wahrscheinlichkeiten liefert, wurde für diese Reaktionen die Wahrscheinlichkeit auf 6% der vom Netz gelieferten Wahrscheinlichkeit herabgesetzt. Mit den so erstellten Regeln erhält man das in Abbildung
47 gezeigte simulierte Spektrum.
-Spaltungen nicht für Spaltungen nach Wasserstoffumlagerungen trainiert wurde und es in diesen Fällen für die Abspaltung
von Wasserstoffradikalen viel zu hohe Wahrscheinlichkeiten liefert, wurde für diese Reaktionen die Wahrscheinlichkeit auf 6% der vom Netz gelieferten Wahrscheinlichkeit herabgesetzt. Mit den so erstellten Regeln erhält man das in Abbildung
47 gezeigte simulierte Spektrum.
 -Spaltungen nach einer Wasserstoffumlagerung vorherzusagen.
An den Intensitäten sind aber noch Verbesserungen nötig und auch die Signale bei einer Masseneinheit höher, die von den
-Spaltungen nach einer Wasserstoffumlagerung vorherzusagen.
An den Intensitäten sind aber noch Verbesserungen nötig und auch die Signale bei einer Masseneinheit höher, die von den  -Spaltungen in die andere Richtung stammen und im Massenspektrometer nicht vorkommen, müßten
ausgeschlossen werden. Für eine Ähnlichkeitssuche, für die dieses Experiment durchgeführt wurde, könnte das simulierte Spektrum möglicherweise dennoch ausreichen.
-Spaltungen in die andere Richtung stammen und im Massenspektrometer nicht vorkommen, müßten
ausgeschlossen werden. Für eine Ähnlichkeitssuche, für die dieses Experiment durchgeführt wurde, könnte das simulierte Spektrum möglicherweise dennoch ausreichen. -Spaltungen
in die falsche Richtung aus, kann das simulierte Spektrum verbessert werden.
-Spaltungen
in die falsche Richtung aus, kann das simulierte Spektrum verbessert werden.  -Spaltungen ausgeschlossen, bei denen kein Radikal als Neutralfragment abgespalten wird, wodurch die
-Spaltungen ausgeschlossen, bei denen kein Radikal als Neutralfragment abgespalten wird, wodurch die  -Spaltungen in die falsche Richtung verhindert werden. Die Gleichgewichtskonstanten der
Wasserstoffumlagerung auf ein Kohlenstoffatom wurden für 5-gliedrige Übergangszustände auf 0.16, für 6-gliedrige auf 0.35 und für 7-gliedrige auf 0.08 gesetzt. Für die Wasserstoffumlagerung auf ein Heteroatom wurde nur eine 1,3-Wasserstoffverschiebung
erlaubt, die sicher als zwei 1,2-Verschiebungen entlang des
-Spaltungen in die falsche Richtung verhindert werden. Die Gleichgewichtskonstanten der
Wasserstoffumlagerung auf ein Kohlenstoffatom wurden für 5-gliedrige Übergangszustände auf 0.16, für 6-gliedrige auf 0.35 und für 7-gliedrige auf 0.08 gesetzt. Für die Wasserstoffumlagerung auf ein Heteroatom wurde nur eine 1,3-Wasserstoffverschiebung
erlaubt, die sicher als zwei 1,2-Verschiebungen entlang des 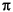 -Systems der Säure oder des Esters stattfindet. Die Gleichgewichtskonstante wurde abhängig von der Größe des Kations so bestimmt, daß sich für
Decansäureethylester (38 Atome) ein Wert von 0.08 ergibt und für Methylstearat (59 Atome) 0.28. Das Spektrum von Decansäureethylester ist in Abbildung 48 gezeigt.
-Systems der Säure oder des Esters stattfindet. Die Gleichgewichtskonstante wurde abhängig von der Größe des Kations so bestimmt, daß sich für
Decansäureethylester (38 Atome) ein Wert von 0.08 ergibt und für Methylstearat (59 Atome) 0.28. Das Spektrum von Decansäureethylester ist in Abbildung 48 gezeigt.



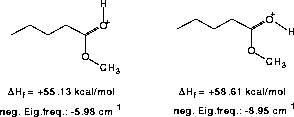
![[Prev]](p_prev.gif)
![[Next]](p_next.gif)