![[Prev]](p_prev.gif)
![[Next]](p_next.gif)
4.2. Erstellung der Wissensbasis
Die Wissensbasis besteht aus den Regeln, in denen die verschiedenen Fragmentierungs- und Umlagerungstypen kodiert sind. Für die Analyse von Massenspektren enthalten die Regeln keine Reaktivitätsbewertung.
4.2.1. Fragmentierungsregeln
Begonnen wurde mit den Fragmentierungs- und Umlagerungsreaktionen, wie sie in Abbildung 7 gezeigt sind, sowie der n- und 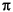 -Ionisation. Angaben wie 3-7 besagen, daß an dieser Stelle eine Kette von
Atomen einer Länge zwischen drei und sieben ist. Dies ist der Satz aller möglichen Reaktionstypen. Welche Reaktionen auch tatsächlich im Massenspektrometer stattfinden und in welchem Ausmaß, wird von FRANZ (Fragmentation and Rearrangement
ANalyZer) aus den Reaktionstypen, dem experimentellen Massenspektrum und der Struktur der Verbindung ermittelt [23][24]. Ergebnis der Berechnungen von FRANZ sind dann Datenbanken
für die einzelnen Reaktionstypen mit Reaktionen diesen Typs, denen eine Reaktionswahrscheinlichkeit zugeordnet ist.
-Ionisation. Angaben wie 3-7 besagen, daß an dieser Stelle eine Kette von
Atomen einer Länge zwischen drei und sieben ist. Dies ist der Satz aller möglichen Reaktionstypen. Welche Reaktionen auch tatsächlich im Massenspektrometer stattfinden und in welchem Ausmaß, wird von FRANZ (Fragmentation and Rearrangement
ANalyZer) aus den Reaktionstypen, dem experimentellen Massenspektrum und der Struktur der Verbindung ermittelt [23][24]. Ergebnis der Berechnungen von FRANZ sind dann Datenbanken
für die einzelnen Reaktionstypen mit Reaktionen diesen Typs, denen eine Reaktionswahrscheinlichkeit zugeordnet ist.
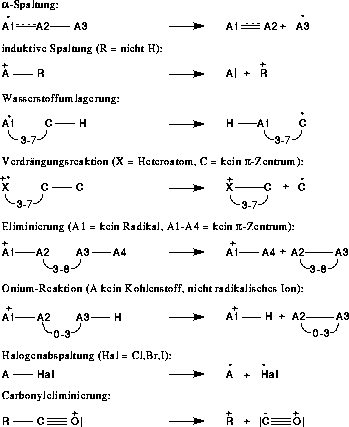
Abbildung 7: Regeln unter Verwendung der Wasserstoffumlagerung.
Diese Fragmentierungs- und Umlagerungstypen sind der Literatur entnommen [1]. Die Carbonyleliminierung entspricht der Kodierung einer induktiven Spaltung aus einer anderen mesomeren Grenzstruktur. Nimmt man die Grenzstruktur,
bei der die positive Formalladung am Kohlenstoffatom lokalisiert ist und nur eine Doppelbindung zum Sauerstoffatom besteht, handelt es sich um eine induktive Spaltung.
4.2.2. Datengewinnung mit FRANZ
Ausgehend vom experimentellen Massenspektrum, der chemischen Struktur der Substanz und den Ionisations-, Fragmentierungs- und Umlagerungstypen erzeugt FRANZ das Netzwerk der im Massenspektrometer ablaufenden Reaktionen. Nach jeder Reaktion bestimmt FRANZ, ob
das Produktkation im Massenspektrum beobachtet wird oder nicht. Für die Kationen, die auch im Spektrum zu sehen sind, werden weitere Reaktionen durchgeführt, bis entweder vom Kation keine Reaktionen mehr stattfinden können oder die Produktkationen
eine kleinere Masse besitzen als das Signal mit der geringsten Masse im Massenspektrum. Für die Reaktionen im zweiten Fall kann keine Aussage über die Reaktivität gemacht werden, da die Massenspektren in vielen Fällen im Bereich niedriger
Massen abgeschnitten sind. Um auch schnelle Folgereaktionen erkennen zu können, bei denen die Masse des Zwischenprodukts nicht im Spektrum zu sehen ist, wird auch von Produkten, deren Signale nicht zu sehen sind, noch eine Reaktionsebene erzeugt. Sind
auch deren Produkte nicht im Massenspektrum zu sehen, werden sie verworfen.
Da einige Massenspektren bei fast allen Massen im Spektrum mindestens ein Signal von bis zu zwei Prozent haben, kann bei FRANZ ein Schwellwert eingestellt werden, ab dem ein Signal als gesichert im Massenspektrum enthalten angesehen wird.
Ist das ganze Reaktionsnetzwerk erzeugt, werden die Umlagerungssysteme zusammengefaßt, da ihre Ionen im Massenspektrum nicht unterschieden werden können, und für alle Fragmentierungen aus den Signalintensitäten im Massenspektrum die Reaktionswahrscheinlichkeiten
berechnet. Da auch verschiedene Reaktionswege zu gleichen oder gleichschweren Kationen führen können, kann nicht für jede Reaktion eine eindeutige Reaktionswahrscheinlichkeit bestimmt werden. FRANZ ermittelt deshalb für jede Reaktion auch
eine Unter- und Obergrenze für die Wahrscheinlichkeit. Ob die ermittelte Reaktionswahrscheinlichkeit eher an der Ober- oder Untergrenze liegt, wird durch Heuristiken festgelegt (siehe 4.2.2.4).
4.2.2.1. Reaktionswahrscheinlichkeiten
Die Reaktionswahrscheinlichkeiten werden aus den Intensitäten der Signale des experimentellen Massenspektrums berechnet. Zur Ableitung der Reaktionswahrscheinlichkeiten werden Massenspektren aus Datenbanken verwendet, die oft nicht die zu fordernden Qualitätskriterien
aufweisen. So werden die Massenspektren meist unterhalb einer Masse von m/z 20 bis 40 abgeschnitten und manchmal enthalten die Massenspektren bei fast jeder Masse zwar ein sehr kleines, aber wahrnehmbares Signal. Dies wird von FRANZ dadurch berücksichtigt,
daß Reaktionen, deren Produktkationen eine kleinere als die minimale beobachtete Masse im Spektrum besitzen, nicht berücksichtigt werden und Signale mit einer Intensität unterhalb eines Schwellwerts als nicht sicher im Massenspektrum enthalten
angesehen werden. Da meist auch die Intensitäten der Isotopensignale, die zur Aufteilung der Intensitäten der Signale auf nicht isomere Kationen gleicher Masse verwendet werden, geringer als die theoretischen Werte sind, wird vor der Auswertung zu
Signalen mit einer geringeren Intensität ein kleiner Betrag hinzuaddiert, z.B. 0.5 bei Signalen bis zu einer Intensität von 9 .
Nachdem alle Ionen, die durch Umlagerungen miteinander verknüpft sind, zu einer virtuellen Struktur - dem Umlagerungssysteme - zusammengefaßt wurden, werden für die Reaktionen über die folgende Gleichung die Reaktionswahrscheinlichkeiten
Pi berechnet. Die Gleichung entspricht einer Kinetik erster Ordnung, Ui sind die Umsätze und zi die Symmetriezahlen für die von A ausgehenden Reaktionen, [A]0 die Anfangskonzentration und [A]t die Restkonzentration der Ausgangsverbindung nach dem
betrachteten Reaktionszeitraum [25].
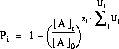
In gleicher Weise werden auch die Unter- und Obergrenzen berechnet, wobei der Aufbau des Reaktionsnetzwerks, das Auftreten mehrerer Fragmente mit gleicher Masse und der Abgleich der Isotopensignale mit den experimentellen Signalen eine Rolle spielen (siehe
4.2.2.2).
4.2.2.2. Sicherheit der Bewertungen
Es gibt verschiedene Gründe, durch die FRANZ die Möglichkeit genommen werden kann, den Reaktionen eindeutige Wahrscheinlichkeiten zuzuordnen. Wird beispielsweise ein Fragment auf zwei verschiedenen Reaktionswegen gebildet, kann dies vollständig
über den einen, wie auch über den anderen Weg oder einer Mischung aus beiden geschehen.
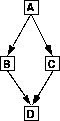
Abbildung 8: Zwei Wege zum gleichen Fragment.
Für jede dieser Reaktionen ist die Untergrenze der Reaktionswahrscheinlichkeit null, wenn die Fragmente B und C nicht im Spektrum zu sehen sind, und die Obergrenze die Wahrscheinlichkeit, wenn das Fragment D ausschließlich über diesen Weg gebildet
wird. Sind die Fragmente B und/oder C im Massenspektrum zu sehen, erhöhen sich die Ober- und Untergrenzen der Reaktionswahrscheinlichkeiten für die Reaktionen A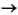 B und A
B und A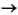 C um den Teil, der der
im Spektrum sichtbaren Fragmente B und C entspricht. Für reaktive Reaktionen mit einer Wahrscheinlichkeit größer ca. 0.7 hat dies zur Folge, daß über diese Reaktion eigentlich keine sichere Aussage für die Reaktionswahrscheinlichkeit
mehr getroffen werden kann, da sie zwischen 0.0 und 0.7 bzw. noch höher liegen, also fast alle Wahrscheinlichkeitswerte besitzen kann.
C um den Teil, der der
im Spektrum sichtbaren Fragmente B und C entspricht. Für reaktive Reaktionen mit einer Wahrscheinlichkeit größer ca. 0.7 hat dies zur Folge, daß über diese Reaktion eigentlich keine sichere Aussage für die Reaktionswahrscheinlichkeit
mehr getroffen werden kann, da sie zwischen 0.0 und 0.7 bzw. noch höher liegen, also fast alle Wahrscheinlichkeitswerte besitzen kann.
Als Güte der Bewertung verwendet FRANZ die Differenz zwischen Unter- und Obergrenze der ermittelten Reaktionswahrscheinlichkeiten. Überschreitet diese Differenz den Wert 0.2 nicht, wird sie der Reaktionendatenbank für Klasse-1-Daten hinzugefügt,
für einen Wert bis 0.4 der für Klasse-2-Daten. Die Grenzwerte von 0.2 und 0.4 sind dabei einstellbar. Darüber hinaus enthält FRANZ auch noch einen Mechanismus, um den Datenraum der Reaktionen möglichst gleichmäßig abzudecken.
Dazu werden die einzelnen Reaktionen in verschiedene Äquivalenzklassen eingeteilt und von Reaktionen einer sehr häufig vorkommenden Klasse wird nur ein Teil der Reaktionen in die Datenbank aufgenommen.
Da solche konkurrierenden Reaktionswege auch systematisch für Verbindungen mit einer bestimmten Substruktur vorkommen können und dann für diese in den von FRANZ erstellten Reaktionsdatenbanken keine Reaktionen enthalten sind, ist bei der Erstellung
der Reaktionstypen darauf zu achten, daß dieser Fall nicht eintreten kann.
Isomere Fragmente können durch ihre gleiche Masse und Isotopensignale im Massenspektrum nicht unterschieden werden. Die Kationen, die ineinander umlagern, werden deshalb - wie schon erwähnt - zu Umlagerungssystemen zusammengefaßt. Haben mehrere
Umlagerungssysteme oder Fragmente außerhalb von Umlagerungssystemen das gleiche Isotopenmuster oder Muster, die sich bezüglich der Intensitätsauflösung nicht unterscheiden, können deren Intensitäten ebenfalls nicht festgestellt
werden. Auch in solchen Fällen ist die Untergrenze der Reaktionswahrscheinlichkeiten der Reaktionen von und zu solchen Fragmenten oder Umlagerungssystemen gleich null. Kann ein Folgefragment eindeutig einer Signalgruppe im Massenspektrum zugeordnet werden,
erhöht sich die Untergrenze auf den Betrag, der nötig ist, um dieses Folgeprodukt zu bilden.
Da bei Umlagerungsreaktionstypen grundsätzlich eine zum Edukt isomere Verbindung entsteht, stellen diese Reaktionstypen eine besondere Schwierigkeit dar. Für diese Reaktionstypen, die immer in Umlagerungssystemen liegen, kann FRANZ nur sehr ungenaue
Reaktionswahrscheinlichkeiten ermitteln, da sich die Signale des Edukts und Produkts im Massenspektrum nicht unterscheiden und somit deren Konzentrationen nicht bestimmt werden können. Stellt FRANZ eine Untergrenze der Wahrscheinlichkeit größer
null fest, wird die Umlagerungsreaktion als reaktiv eingestuft. Analoges gilt für Reaktionen mit einer Obergrenze der Wahrscheinlichkeit von null. Sie werden als nicht reaktiv klassifiziert. FRANZ kann für Reaktionstypen, die eine Umlagerung kodieren,
nur in wenigen Fällen den Reaktionen eine Reaktivität zuordnen, die dann nur angibt, ob diese Umlagerung stattfindet oder nicht. Umlagerungsreaktionstypen haben daneben noch weitere Effekte, die im nächsten Kapitel beschrieben sind.
4.2.2.3. Umlagerungen als Reaktionstyp
Bei der Verwendung der Regeln, die die Wasserstoffumlagerung einschließen, aus Abbildung 7 auf Seite 16 hat sich gezeigt, daß FRANZ fast jedem Signal im Massenspektrum ein Fragment zuordnen kann. Dies erreicht FRANZ
häufig dadurch, daß Wasserstoffatome solange radikalisch umgelagert werden, bis ein Fragment der Masse abgespalten werden kann, das im experimentellen Massenspektrum enthalten ist. Häufig hat dies nicht nur unübersichtliche Reaktionswege
zur Folge, die nur teilweise korrekt sind, sondern bietet oft auch Reaktionswege, bei denen ein Fragment auf mehr als einer Reaktionssequenz gebildet werden kann. Das wiederum hat eine Verringerung der Sicherheit bei der Ermittlung der Reaktionswahrscheinlichkeit
zur Folge.
Ein weiteres Problem erkennt man, wenn man zwei  -Spaltungen betrachtet, die von zwei verschiedenen Fragmenten eines Umlagerungssystems ausgehen. Diese Reaktionen finden beispielsweise im Massenspektrometer bei der Aufnahme der Spektren
von Fettsäuren und deren Estern statt. Abbildung 9 zeigt hierfür ein Beispiel, wobei der unterlegte Teil das nur teilweise gezeigte Umlagerungssystem darstellt. Die Reaktionen unten sind die konkurrierenden
-Spaltungen betrachtet, die von zwei verschiedenen Fragmenten eines Umlagerungssystems ausgehen. Diese Reaktionen finden beispielsweise im Massenspektrometer bei der Aufnahme der Spektren
von Fettsäuren und deren Estern statt. Abbildung 9 zeigt hierfür ein Beispiel, wobei der unterlegte Teil das nur teilweise gezeigte Umlagerungssystem darstellt. Die Reaktionen unten sind die konkurrierenden  -Spaltungen.
-Spaltungen.
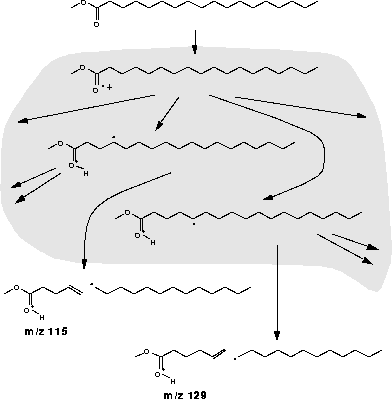
Abbildung 9: Konkurrierende  -Spaltungen aus einem Umlagerungssystem.
-Spaltungen aus einem Umlagerungssystem.
Da FRANZ, wie schon in 4.2.2.2 gesagt, keine Konzentrationen für die Fragmente eines Umlagerungssystem berechnen kann, werden die Ionen des Umlagerungssystems zusammengefaßt und FRANZ bestimmt nur die Gesamtkonzentration
aller Umlagerungsprodukte. Daß das rechte Produkt der  -Spaltung (m/z 129) etwa in doppelt bis dreimal so großem Ausmaß gebildet wird wie das linke (m/z 115) (siehe Abbildung 10), kann
sicherlich nicht an den unterschiedlich stark ablaufenden
-Spaltung (m/z 129) etwa in doppelt bis dreimal so großem Ausmaß gebildet wird wie das linke (m/z 115) (siehe Abbildung 10), kann
sicherlich nicht an den unterschiedlich stark ablaufenden  -Spaltungen liegen, da die elektronischen und energetischen Verhältnisse vergleichbar sind. Da FRANZ das Umlagerungssystem zusammenfaßt und nur eine Konzentration
dafür besitzt, verwendet FRANZ diese Konzentration auch als Eduktkonzentration für die Berechnung der Reaktionswahrscheinlichkeiten. Die unterschiedlichen Produkt- und gleichen Eduktkonzentrationen haben verschiedene Reaktionswahrscheinlichkeiten
zur Folge. Dies kann man allerdings nicht, wie oben gesagt wurde, durch die Verhältnisse am Reaktionszentrum erklären. Die unterschiedliche Bildung der Produkte der
-Spaltungen liegen, da die elektronischen und energetischen Verhältnisse vergleichbar sind. Da FRANZ das Umlagerungssystem zusammenfaßt und nur eine Konzentration
dafür besitzt, verwendet FRANZ diese Konzentration auch als Eduktkonzentration für die Berechnung der Reaktionswahrscheinlichkeiten. Die unterschiedlichen Produkt- und gleichen Eduktkonzentrationen haben verschiedene Reaktionswahrscheinlichkeiten
zur Folge. Dies kann man allerdings nicht, wie oben gesagt wurde, durch die Verhältnisse am Reaktionszentrum erklären. Die unterschiedliche Bildung der Produkte der  -Spaltungen liegt vielmehr daran, daß die Wasserstoffumlagerungen
mit unterschiedlichen Reaktivitäten ablaufen und daher zu unterschiedlichen Konzentrationen für die Edukte der nachfolgenden
-Spaltungen liegt vielmehr daran, daß die Wasserstoffumlagerungen
mit unterschiedlichen Reaktivitäten ablaufen und daher zu unterschiedlichen Konzentrationen für die Edukte der nachfolgenden  -Spaltungen führen. Dies kann auch dadurch belegt werden, daß das Signalmuster eines
Fettsäureesters gut reproduziert werden kann (siehe Abbildung 10), wenn ausgehend von den Molekülionen zu 10% eine
-Spaltungen führen. Dies kann auch dadurch belegt werden, daß das Signalmuster eines
Fettsäureesters gut reproduziert werden kann (siehe Abbildung 10), wenn ausgehend von den Molekülionen zu 10% eine  -Spaltung stattfindet und die restlichen 90% eine Wasserstoffumlagerung
eingehen, wobei diese zu 15% über einen 5-, zu 80% über einen 6- und zu 5% über einen 7-gliedrigen Übergangszustand erfolgt und bei allen
-Spaltung stattfindet und die restlichen 90% eine Wasserstoffumlagerung
eingehen, wobei diese zu 15% über einen 5-, zu 80% über einen 6- und zu 5% über einen 7-gliedrigen Übergangszustand erfolgt und bei allen  -Spaltungen ein Alkylradikal abgespalten wird. [47]
-Spaltungen ein Alkylradikal abgespalten wird. [47]
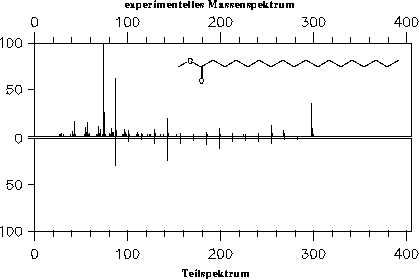
Abbildung 10: Vergleich des Teilspektrums [47], in dem nur die Signale enthalten sind, deren Ionen nur durch Wasserstoffumlagerungen und  -Spaltungen gebildet werden, mit dem experimentellen
Massenspektrum [22] von Methylstearat.
-Spaltungen gebildet werden, mit dem experimentellen
Massenspektrum [22] von Methylstearat.
4.2.2.4. Heuristiken
Da nicht alle gebildeten Fragmente im Massenspektrum unterschieden werden können, benötigt FRANZ einige zusätzliche Annahmen über die stattfindenden Reaktionen. Diese gliedern sich in zwei Gruppen, diejenigen, die Reaktionen, die aufgrund
der Reaktionstypen möglich sind, ausschließen und solche, die nur die angenommene Reaktionswahrscheinlichkeit zwischen der Unter- und Obergrenze beeinflussen, während die Grenzen und damit die Sicherheit der Bewertung unverändert bleiben.
Heuristiken zum Ausschluß von Reaktionen
Eine dieser Heuristiken ist die Beurteilung der cyclischen Übergangszustände hinsichtlich der Ringspannung. Die Bildung eines solchen Übergangszustands wird von FRANZ aus den Definitionen der Reaktionssubstruktur, wenn sie zwei Teilsubstrukturen
enthält, die über eine Kette von Atomen miteinander verbunden sind, und der Reaktion erkannt. Ist die notwendige Flexibilität der Kette durch Mehrfachbindungen oder starre Ringsysteme nicht ausreichend gegeben, wird die Reaktion verworfen.
Daneben ist eine zweimalige radikalische Wasserstoffumlagerung auf eine funktionelle Gruppe bei der Elektronenstoßmassenspektroskopie nur in wenigen Fällen, wie der Abspaltung von Wasser aus Aldehyden (Signal von etwa 1-2%) [47]
oder der doppelten McLafferty-Umlagerung, von Bedeutung. Erstellt man für diese Fälle spezielle Reaktionstypen (Umlagerung mit anschließender Spaltung) und beschränkt die radikalische Wasserstoffumlagerung auf die einmalige Umlagerung auf
eine funktionelle Gruppe (siehe Abbildung 11), reduziert man das Umlagerungsnetzwerk der Wasserstoffumlagerungen auf einen Bruchteil des unbeschränkten Netzwerks ohne nennenswerten Informationsverlust (siehe Abbildung
12). Um von einer Ausgangsstruktur alle möglichen Reaktionen zu finden, ist es notwendig, die Reaktionen aller mesomeren Grenzstrukturen zu generieren.
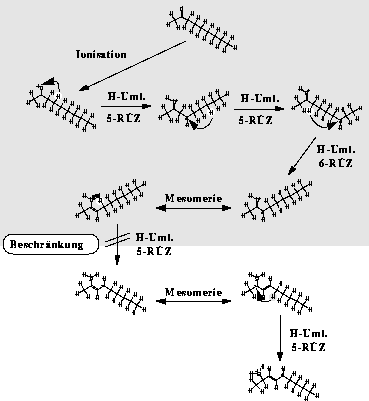
Abbildung 11: Beschränkung der Wasserstoffumlagerung bei 2-Nonanon. Nur der grau unterlegte Teil wird erzeugt. H-Uml. steht für Wasserstoffumlagerung und 5-RÜZ für einen 5-Ring-Übergangszustand.
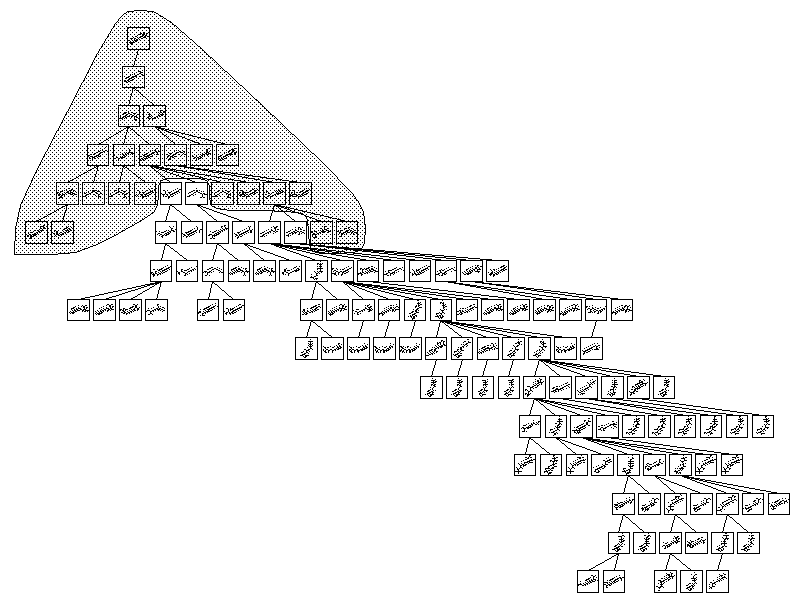
Abbildung 12: n-Ionisation und Umlagerungsnetzwerk des 2-Nonanons. Der unterlegte Teil ist der Teil des beschränkten Netzwerks, wobei das Netzwerk so dargestellt ist, daß jede Reaktion nur einmal gezeichnet ist, aber ein bestimmtes Kation
an mehreren Stellen gebildet werden kann. Ist ein Kation mehrfach enthalten, sind seine Reaktionen nur an einer Darstellung angegeben.
Durch den Ausschluß der Reaktionen einer doppelten radikalischen Wasserstoffumlagerung erhält man bei der Analyse von Massenspektren kleinere Unsicherheitsbereiche bei den Reaktionswahrscheinlichkeiten (siehe 4.2.2.2)
und hat durch die geringere Anzahl von Reaktionen eine kürzere Berechnungszeit sowohl bei der Analyse als auch bei einer möglichen Simulation, die die gewonnenen Fragmentierungsregeln mit Bewertung verwendet.
Heuristiken zur Verteilung der Umsätze
FRANZ führt ausgehend vom Molekülion alle möglichen Fragmentierungs- und Umlagerungsreaktionen durch und bestimmt aus den Signalen im Massenspektrum die Konzentrationen der Kationen. Die Reaktionswahrscheinlichkeiten, die FRANZ den einzelnen
Reaktionen zuordnet, werden aus den Umsätzen bestimmt, die sich aus den Mengen des Kations und aller über dieses gebildeten Ionen ergibt. Die Verteilung der Umsätze ist eine Heuristik, die eingesetzt wird, wenn ein Fragment ausgehend von zwei
oder mehr Umlagerungssystemen bzw. Fragmenten gebildet wird. Hier werden die Umsätze proportional zur Anzahl der Ionen im Umlagerungssystem verteilt. Fragmente, die keinem Umlagerungssystem angehören, haben die Größe eins.
Ist die Anzahl der Reaktionsschritte vom unionisierten Molekül bis zum Fragment, das auf mehreren Wegen gebildet wird, unterschiedlich groß, werden die Umsätze so auf die Reaktionsfolgen verteilt, daß das Ion zum überwiegenden Maße
über den kürzesten Reaktionsweg entsteht. Die Umsätze über die verschiedenen Wege werden um so stärker differenziert, je größer der Unterschied in der Zahl der Reaktionsschritte ist, und sinkt bei gleichem Unterschied mit
der Zahl der Folgereaktionen.
Daneben kann FRANZ die Reaktionswahrscheinlichkeiten nach Möglichkeit auch an vorgegebene Werte angleichen. Dies setzt voraus, daß man für alle Reaktionen auch brauchbare Werte für die Wahrscheinlichkeiten hat. So können die Bewertungen
der Reaktionen schrittweise verbessert werden. Für die Entwicklung der ersten Wahrscheinlichkeitsfunktionen bzw. neuronalen Netze, die in dieser Arbeit vorgestellt werden, kann man dieses Feature jedoch nicht heranziehen.
4.2.3. Modifikation der Regeln
Bei näherer Betrachtung der Reaktions- und Umlagerungsnetzwerke, die FRANZ für verschiedene Verbindungen ausgehend von ihrem Massenspektrum erzeugt hat, fiel auf, daß FRANZ fast alle Signale im Spektrum erklären konnte, dies aber häufig
nur über Wasserstoffumlagerungen erreichte. Da diese für die Ableitung von Bewertungsfunktionen zur Vorhersage von Massenspektren Schwierigkeiten machen (siehe 4.2.2.3), wurden die Wege, auf denen die Fragmente gebildet
werden, genauer untersucht und die Reaktionsregeln daraufhin modifiziert.
4.2.3.1. Weiterentwicklung
Es wurde festgestellt, daß einige Fragmente ausschließlich über Wasserstoffumlagerungen mit großen Ringübergangszuständen erzeugt werden können und daher einen geringen Umsatz aufweisen sollten. Die Wasserstoffumlagerung war
für sechs- bis zehngliedrige Ringübergangszustände zugelassen. Sie wurden auf fünf- bis siebengliedrige Ringe beschränkt, bei denen die Reaktionen sowohl enthalpisch, wie auch entropisch im günstigen Bereich liegen. Diese Ringgrößen
haben sich auch für die Simulation als geeignet erwiesen (siehe Abbildung 10 auf Seite 21). Um für die Umlagerungen auf Heteroatome, die exotherm und somit begünstigt sind, auch 1,2-Wasserstoffverschiebungen
zuzulassen, wurden Umlagerungen für diese über drei- bis siebengliedrige Ringe erlaubt. Umlagerungen über viergliedrige Ringe, die energetisch am ungünstigsten sind, konnten beim Reaktionsgenerator von FRANZ und MASSIMO nicht ausgeschlossen
werden. Zusammengefaßt kann gesagt werden, daß die radikalische Wasserstoffumlagerung für große Ringübergangszustände beschränkt und gleichzeitig um Umlagerungen mit kurzen Distanzen ergänzt wurde.
Daneben wurden induktive Spaltungen, deren positive Ladung an einem Kohlenstoffatom lokalisiert ist, ausgeschlossen, da sie bei der Fragmentierung im Massenspektrometer eine untergeordnete Rolle spielen. Werden FRANZ auch solche Reaktionsmöglichkeiten,
bei denen Carbene entstehen, angeboten, entstehen oft alternative Reaktionssequenzen zu gleichschweren Ionen, was FRANZ die Möglichkeit der eindeutigen Zuordnung von Reaktionswahrscheinlichkeiten nimmt.
Gleichschwere Kationen, wie die der Carbene, werden durch eine 1,2-Eliminierung von Wasserstoffmolekülen gebildet [27]. Deshalb wurde der Reaktionstyp von Abbildung 13 den Regeln
hinzugefügt.
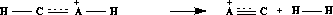
Abbildung 13: Abspaltung molekularen Wasserstoffs.
Damit von FRANZ bei primären Alkoholen nicht systematisch alternative Reaktionswege und damit unsichere Reaktionswahrscheinlichekeiten zur Bildung des R-C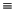 O+-Ions und aller seiner Folgeprodukte, der Serie der Alkylfragmente,
gefunden werden, wurde diese Reaktion ausgeschlossen, wenn das Radikalzentrum und die positive Ladung an einem Atom lokalisiert sind (siehe Abbildung 14). Ohne diesen Ausschluß könnten die
O+-Ions und aller seiner Folgeprodukte, der Serie der Alkylfragmente,
gefunden werden, wurde diese Reaktion ausgeschlossen, wenn das Radikalzentrum und die positive Ladung an einem Atom lokalisiert sind (siehe Abbildung 14). Ohne diesen Ausschluß könnten die  -Spaltung
(Abspaltung eines Wasserstoffradikals) und die Eliminierung von Wasserstoffmolekülen in beiden Reihenfolgen auf das Molekülion angewendet werden, wobei das R-C
-Spaltung
(Abspaltung eines Wasserstoffradikals) und die Eliminierung von Wasserstoffmolekülen in beiden Reihenfolgen auf das Molekülion angewendet werden, wobei das R-C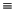 O+-Ion entsteht, und FRANZ könnte für die Reaktionen
keine sicheren Reaktionswahrscheinlichkeiten berechnen (siehe 4.2.2.2).
O+-Ion entsteht, und FRANZ könnte für die Reaktionen
keine sicheren Reaktionswahrscheinlichkeiten berechnen (siehe 4.2.2.2).
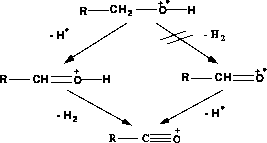
Abbildung 14: Alternative Reaktionswege bei primären Alkoholen.
Durch die Einführung der Eliminierung von Wasserstoffmolekülen können auch die Signale M-1 und M-3 im Spektrum von Methanol (Abbildung 15) erklärt werden. M steht dabei für die Molekülmasse. Das
kleine Signal bei M-2 muß der sicheren Ermittlung der Reaktionswahrscheinlichkeiten durch FRANZ geopfert werden, da keine Möglichkeit bestand, selektiv die Weiterreaktion des Fragmentes mit der Masse M-2 zu verhindern. Dies ist allerdings nur von
geringer Bedeutung, da die Signale bei M-1, M-2 und M-3 bei längeren Alkylketten ohnehin nicht mehr in den Spektren enthalten sind.

Abbildung 15: Massenspektrum von Methanol.
Analoges gilt für die Spektren der Verbindungen Methylmercaptan (Abbildung 16) und Methylamin (Abbildung 17).
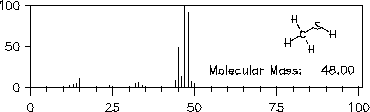
Abbildung 16: Massenspektrum von Methylmercaptan.
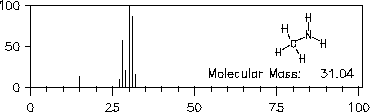
Abbildung 17: Massenspektrum von Methylamin.
Das für primäre Alkohole gebildete R-C O+-Ion spaltet Kohlenmonoxid ab und fragmentiert danach wie Alkylkationen. Dazu wird der Reaktionstyp der induktiven
O+-Ion spaltet Kohlenmonoxid ab und fragmentiert danach wie Alkylkationen. Dazu wird der Reaktionstyp der induktiven  -Spaltung benötigt [27],
der ebenfalls neu eingeführt wurde.
-Spaltung benötigt [27],
der ebenfalls neu eingeführt wurde.

Abbildung 18: Induktive  -Spaltung.
-Spaltung.
Die Carbonyleliminierung, die nur einen Spezialfall der induktiven Spaltung aus einer anderen mesomeren Grenzstruktur darstellt, wurde so erweitert, daß an Stelle des Sauerstoffatoms auch andere Heteroatome stehen können. Diese Reaktionen finden bei
der Fragmentierung von Nitrilen und Aminen Anwendung [18].
Desweiteren wurde die Eliminierung aus dem Satz möglicher Reaktionstypen genommen, da sie nur in Spezialfällen entscheidende Signale im Massenspektrum erklärt. Die Verdrängungsreaktion wurde für ionisierte Carbonylverbindungen ausgeschlossen,
da dieser Reaktionstyp für derartige Verbindungen nicht stattfindet, sowie zur Bildung von dreigliedrigen Ringen zugelassen, die in [18] beschrieben sind und in den Massenspektren von Alkylhalogeniden mit Signalen
von 10% und mehr zu sehen sind. Außerdem wurde die Halogenspaltung so erweitert, daß auch Halogenwasserstoffkationen abgespalten werden können.
Die Reaktionstypen der n- und 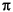 -Ionisation, sowie die
-Ionisation, sowie die  -Spaltung und die Oniumspaltung blieben unverändert. Der sich daraus ergebende Regelsatz ist in Abbildung 19 gezeigt.
-Spaltung und die Oniumspaltung blieben unverändert. Der sich daraus ergebende Regelsatz ist in Abbildung 19 gezeigt.
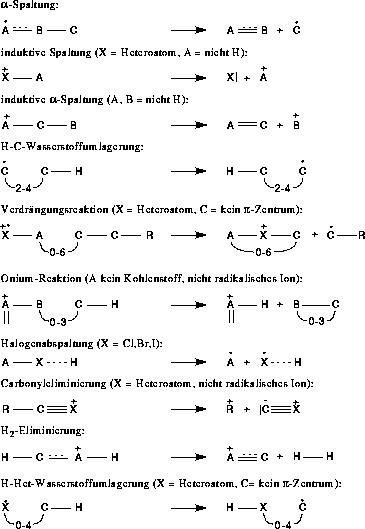
Abbildung 19: Weiterentwickelter Regelsatz.
4.2.3.2. Erhöhung der Genauigkeit der Reaktionswahrscheinlichkeiten
Um Regeln zu erhalten, an denen gezeigt werden konnte, daß mit diesem Ansatz Massenspektren simuliert werden können, wurden die verwendeten Reaktionstypen so modifiziert, daß die oben beschriebenen Schwierigkeiten bei der Zuweisung von Reaktionswahrscheinlichkeiten
(siehe 4.2.2.2) durch FRANZ nicht auftreten sollten. Redundante Reaktionswege zum gleichen Fragment bzw. zu einem gleichschweren Ion und die in Kapitel 4.2.2.3 beschriebenen Probleme mit
Umlagerungsreaktionstypen wurden vermieden, indem beide Reaktionstypen der Wasserstoffumlagerung (auf Kohlenstoff- bzw. Heteroatome) aus dem Satz möglicher Reaktionstypen entfernt wurden. Um nicht einen größeren Prozentsatz der Signale im Massenspektrum
von der Aufklärung durch FRANZ auszuschließen, wurden stattdessen Reaktionstypen eingeführt, die die Wasserstoffumlagerung und die anschließende Fragmentierung in sich vereinen. So wurden die Typen der McLafferty-Spaltung, die eine Wasserstoffumlagerung
und eine sich anschließende  -Spaltung darstellt, und der HX-Eliminierung eingeführt, hinter der sich die Wasserstoffumlagerung mit nachgeschalteter induktiver Spaltung verbirgt. Diese beiden Reaktionstypen sind in Abbildung
20 dargestellt. X ist ein Heteroatom.
-Spaltung darstellt, und der HX-Eliminierung eingeführt, hinter der sich die Wasserstoffumlagerung mit nachgeschalteter induktiver Spaltung verbirgt. Diese beiden Reaktionstypen sind in Abbildung
20 dargestellt. X ist ein Heteroatom.
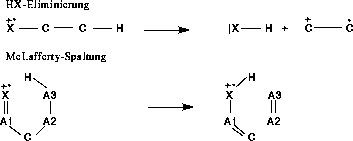
Abbildung 20: McLafferty-Spaltung und HX-Eliminierung.
Bei der McLafferty-Spaltung ist noch zu beachten, daß es sich beim dritten Atom um Kohlenstoff (C in Abbildung 20) handeln muß. Der Grund dafür liegt im untersuchten Datensatz von Molekülen (siehe Anhang
C), der Ester enthält, bei denen eine McLafferty-Spaltung sowohl auf der Säure- wie auch auf der Alkoholseite stattfinden kann. Tritt beim betrachteten Ester eine doppelte McLafferty-Spaltung ein, kann FRANZ
nicht entscheiden, in welcher Reihenfolge die McLafferty-Spaltungen stattfinden. Um die Situation der alternativen Reaktionswege zu vermeiden, wurde die McLafferty-Spaltung nur auf der Seite der Säure gestattet.
Da auch die Verdrängungsreaktion und die Halogenspaltung FRANZ in einigen Fällen alternative Reaktionswege eröffnen und somit in diesen Fällen keine eindeutigen Reaktionswahrscheinlichkeiten ermittelt werden könnten, wurden auch diese
Reaktionstypen aus den Regeln entfernt, obgleich der Datensatz Halogenide enthält. Diese Halogenide wurden im Datensatz belassen, damit die Reaktivitätsfunktionen für die  -Spaltung und die induktive Spaltung auch für
die Halogenide gültig sind. Dies hat zur Folge, daß einige Signale für die halogenhaltigen Substanzen von FRANZ nicht erklärt werden können, aber die durchgeführten Reaktionen werden richtig bewertet, wenn, wie im Fall der Verdrängungsreaktionen,
die Folgereaktionen nur von geringer Bedeutung sind oder, wie im Fall der Halogenspaltung, die Reaktionen nur vernachlässigbare Umsätze besitzen, da im Datensatz nur Monohalogenide enthalten sind.
-Spaltung und die induktive Spaltung auch für
die Halogenide gültig sind. Dies hat zur Folge, daß einige Signale für die halogenhaltigen Substanzen von FRANZ nicht erklärt werden können, aber die durchgeführten Reaktionen werden richtig bewertet, wenn, wie im Fall der Verdrängungsreaktionen,
die Folgereaktionen nur von geringer Bedeutung sind oder, wie im Fall der Halogenspaltung, die Reaktionen nur vernachlässigbare Umsätze besitzen, da im Datensatz nur Monohalogenide enthalten sind.
4.2.4. Berechnung physikochemischer Effekte
Grundlage für die Berechnung der Reaktivitäten sind die physikochemischen Eigenschaften am Reaktionszentrum, der Reaktionssubstruktur in den Edukten. Im Arbeitskreis von Professor Gasteiger wurden in den letzten 20 Jahren empirische Verfahren entwickelt,
die energetische und elektronische Eigenschaften schnell berechnen können.
Zu den Eigenschaften zählen die Polarisierbarkeiten der Atome und Bindungen [28], die Partialladungen und die Elektronegativitäten. Diese werden über das PEOE-Verfahren (partial equalization of orbital electronegativity)
berechnet. So erhält man die 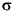 -Partialladungen und
-Partialladungen und 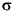 -Restelektronegativitäten der Atome [29][30]. Die Verteilung der
Elektronen in
-Restelektronegativitäten der Atome [29][30]. Die Verteilung der
Elektronen in 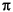 -Systemen basiert auf dem Konzept der Orbitalelektronegativitäten [31].
-Systemen basiert auf dem Konzept der Orbitalelektronegativitäten [31].
Zur Beschreibung der Resonanzeffekte zur Stabilisierung von Ladungen (+M und -M-Effekte) sowie zur Quantifizierung von Hyperkonjugationseffekten existieren Methoden, die den Grad der Delokalisation bestimmen [32]. Bei
der Verbesserung der Verfahren zur Bestimmung der Delokalisation von Ladungen wurde festgestellt, daß für eine optimale Beschreibung die für die Strukturrepräsentation verwendete, chemische Datenstruktur der Atom- und Bindungslisten nicht
geeignet ist, da sie keine dreidimensionale Information über die Moleküle enthält, die für die Abschätzung der Überlappungsintegrale Voraussetzung wären [33]. Dieses Defizit wird teilweise
durch die Einführung einer Datenstruktur wie RICOS (siehe Kapitel 5) beseitigt. Das Berechnungsverfahren müßte dazu allerdings grundlegend überarbeitet werden.
Die Berechnung von Bildungswärmen und Bindungsdissoziationsenergien, die zunächst auf acyclische, organische Substanzen beschränkt war [34], wurde auf ringförmige, neutrale, organische Verbindungen
[35] sowie auf Radikale, Kationen und Radikalkationen erweitert [36][37], wie sie in der Elektronenstoßmassenspektroskopie auftreten. Jedoch
sind auch hier die Abweichungen von den experimentell bestimmten Werten von Bildungsenthalpien für diejenigen ionisierten Moleküle größer als der tolerierbare Fehler, die orthogonale 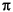 -Systeme und freie Elektronenpaare
enthalten. Hier gibt es Schwierigkeiten zu erkennen, welche Elektronensysteme miteinander konjugiert sind und welche nicht. Zusätzlich kann in der Bindungsliste in solchen Fällen oft nicht eindeutig ein bestimmtes Elektronensystem spezifiziert werden,
aus dem bei der Ionisation das Elektron entfernt wurde. Für die übrigen Verbindungen liegen die Abweichungen von den experimentellen Werten etwa in der Größenordnung der Meßgenauigkeit. Zur Vermeidung dieser Abweichungen ist eine Verbesserung
der Darstellung der chemischen Struktur sowie eine Neugestaltung des Algorithmus für die Berechnung erforderlich. Als Beispiel hierfür dienen ionisierte, ungesättigte Verbindungen, bei denen ein freies Elektronenpaar mit dem
-Systeme und freie Elektronenpaare
enthalten. Hier gibt es Schwierigkeiten zu erkennen, welche Elektronensysteme miteinander konjugiert sind und welche nicht. Zusätzlich kann in der Bindungsliste in solchen Fällen oft nicht eindeutig ein bestimmtes Elektronensystem spezifiziert werden,
aus dem bei der Ionisation das Elektron entfernt wurde. Für die übrigen Verbindungen liegen die Abweichungen von den experimentellen Werten etwa in der Größenordnung der Meßgenauigkeit. Zur Vermeidung dieser Abweichungen ist eine Verbesserung
der Darstellung der chemischen Struktur sowie eine Neugestaltung des Algorithmus für die Berechnung erforderlich. Als Beispiel hierfür dienen ionisierte, ungesättigte Verbindungen, bei denen ein freies Elektronenpaar mit dem 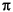 -System
(teilweise) konjugiert ist, wie bei den Jodtoluolen, Brombenzol oder 1,1-Difluorethen. Aber auch bei ionisierten Chinonen treten bei bestimmten mesomeren Grenzstrukturen starke Abweichungen auf. Für diese Substanzen sind Differenzen bei der Bildungswärme
von ca. 200 bis 600 kJ/mol zu beobachten. Legt man der Berechnung der Bildungswärmen eine chemische Datenstruktur zugrunde, bei der die Konjugation von Doppel- und Dreifachbindungen sowie von freien Elektronenpaaren Bestandteil der chemischen Datenstruktur
ist, müßten diese Probleme bewältigt werden können. Aus der Differenz der Bildungswärmen der Produkte und Edukte läßt sich auch die Reaktionsenthalpie berechnen.
-System
(teilweise) konjugiert ist, wie bei den Jodtoluolen, Brombenzol oder 1,1-Difluorethen. Aber auch bei ionisierten Chinonen treten bei bestimmten mesomeren Grenzstrukturen starke Abweichungen auf. Für diese Substanzen sind Differenzen bei der Bildungswärme
von ca. 200 bis 600 kJ/mol zu beobachten. Legt man der Berechnung der Bildungswärmen eine chemische Datenstruktur zugrunde, bei der die Konjugation von Doppel- und Dreifachbindungen sowie von freien Elektronenpaaren Bestandteil der chemischen Datenstruktur
ist, müßten diese Probleme bewältigt werden können. Aus der Differenz der Bildungswärmen der Produkte und Edukte läßt sich auch die Reaktionsenthalpie berechnen.
Neben diesen Eigenschaften können auch rein formale Parameter der Atome, Bindungen und Moleküle für die Berechnung der Reaktivität herangezogen werden. Dazu gehören die Zugehörigkeit von Atomen zu Ringen in der Struktur, wozu neben
dem kompletten Satz von Ringen auch der kleinste Satz kleinster Ringe (SSSR, smallest set of smallest rings [38][39]) bestimmt wird. Aber auch die Beteiligung an einem aromatischen
System [36], die Zahl der Nachbaratome, der Wasserstoff- bzw. Nicht-Wasserstoff-Atome, Indikatoren, die die Möglichkeit der Bildung bzw. des Bruchs von Bindungen angeben, welche auf einer Valenztabelle beruhen, sowie
einige weitere formale Parameter stehen zur Beschreibung des Reaktionszentrums zur Verfügung.
All diese Parameter werden vom eingebauten Subsystem PETRA (Parameter Estimation for the Treatment of Reactivity Applications) berechnet, das für die Reihenfolge der Ermittlung der verschiedenen Eigenschaften auch die Abhängigkeiten der einzelnen
Berechnungsverfahren untereinander berücksichtigt. Dieses Subsystem wird in EROS6 und MASSIMO für die Ermittlung der physikochemischen Eigenschaften eingesetzt, die zur Evaluierung der Reaktivitäten verwendet werden.
4.2.5. Ableitung der Wahrscheinlichkeitsfunktionen
Nachdem die Reaktionstypen festgelegt wurden und mit FRANZ aus den Massenspektren zusammen mit deren Strukturen Reaktionsdatenbanken inklusive der Bewertungen der Reaktionen erstellt wurden, kann man den Zusammenhang zwischen den Eigenschaften der Reaktionssubstruktur
und den Reaktivitäten der Reaktionen herleiten. Dies können Wahrscheinlichkeitsfunktionen bzw. neuronale Netze sein. Dazu werden zunächst die Reaktionen, die der Klasse-1 zugeteilt wurden, für einen Reaktionstyp aus der Datenbank extrahiert
und die physikochemischen Parameter für die Atome und Bindungen am Reaktionszentrum sowie die Eigenschaften der Moleküle berechnet. Das sind 11 Parameter pro Atom im Edukt und im Produkt, 12 Parameter je Bindung im Edukt oder Produkt, 1 Parameter
je Edukt und Produkt sowie die Kettenlänge für jeden Reaktionstyp mit definierter Atomkette und die Zahl der Atome im Edukt. So erhält man einen Datensatz, bei dem jede Reaktion durch alle möglichen Parameter beschrieben wird, auch wenn
diese auf die Beschreibung der Reaktivitäten der Reaktionen keinen Einfluß haben. Deshalb werden vor der Anwendung einer multilinearen Regressionsanalyse oder dem Training neuronaler Netze Variablen (Parameter) mit der Varianz null für den gesamten
Datensatz (alle Reaktionen) sowie linear abhängige Variablen und Variablen mit einer Korrelation größer 0.98 (bzw. 0.8) entfernt. Da einige Parameter systematisch linear abhängig sind, gibt es eine Liste bevorzugt verwendeter Parameter zur
Entscheidung, welcher der linear abhängigen oder hoch korrelierten Parameter verworfen wird. Zu den systematisch linear abhängigen Eigenschaften gehören beispielsweise die Differenz der 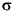 -Elektronegativitäten zweier
benachbarter Atome im Reaktionszentrum und die
-Elektronegativitäten zweier
benachbarter Atome im Reaktionszentrum und die 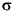 -Elektronegativitäten dieser Atome.
-Elektronegativitäten dieser Atome.
4.2.5.1. Regeln mit Umlagerungsreaktionstypen
Bei den Datensätzen, die sich ergeben, wenn der Satz von Reaktionstypen auch Umlagerungsreaktionstypen enthält, lassen sich zwischen den physikochemischen Parametern und den Reaktivitäten keine linearen Zusammenhänge finden. Für eine
optimale Regression, bei der nur signifikante Variablen verwendet werden, erhält man ein Diagramm, bei dem die vorhergesagten gegen die von FRANZ bestimmten Reaktionswahrscheinlichkeiten aufgetragen sind, wie es in Abbildung
21 gezeigt ist. Der Korrelationskoeffizient von 0.5964 zeigt bei 9 signifikanten Variablen an, daß diese Regression unbrauchbar ist. Als Beispiel dient der Datensatz der Carbonyleliminierungsreaktionen (siehe Anhang D.1.1).
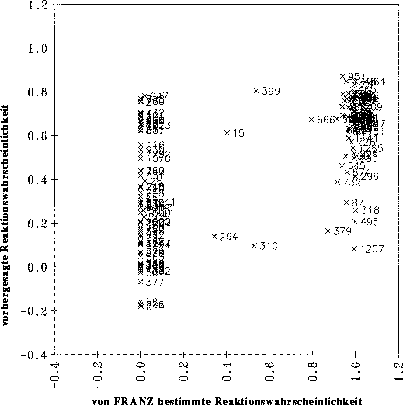
Abbildung 21: Diagramm, bei der die mit einer multilinearen Regression vorhergesagten Reaktionswahrscheinlichkeiten gegen die von FRANZ bestimmten (Sollwerte) aufgetragen sind. 139 Datenpunkte. Die Nummern der Datenpunkte sind die Nummern der Reaktionen
im Anhang D.1.1.
Auch bei der Verwendung von 24 Variablen, von denen nur 9 als signifikant einzustufen sind, ergibt sich lediglich eine Steigerung des Korrelationskoeffizienten r von 0.5964 auf 0.6483.
Neben den richtig klassifizierten Reaktionen enthält ein Datensatz auch Reaktionen mit durch Umlagerungsreaktionstypen von FRANZ falsch bestimmte Reaktionswahrscheinlichkeiten (siehe 4.2.2.3), die bis zu etwa zehn Prozent
der Datenpunkte ausmachen. So besteht die Schwierigkeit, daß weder der Satz der Datenpunkte mit korrekter Reaktionswahrscheinlichkeit noch der Satz der Parameter bekannt ist, die die Abhängigkeit der Reaktionswahrscheinlichkeit beschreiben. Kennt
man entweder die korrekten Datenpunkte oder die entscheidenden Variablen, gibt es etablierte Methoden zur Ermittlung der gewünschten Datenpunkte bzw. Parameter. Unternimmt man einen Versuch durch chemisches Wissen die höchst wahrscheinlich von FRANZ
fehlklassifizierten Datenpunkte zu identifizieren und aus dem Datensatz zu entfernen, reduziert sich dadurch der Datensatz auf 115 Datenpunkte. So kann man die Qualität der Korrelation deutlich steigern (siehe Abbildung 22),
obgleich sie noch weit von einem genügend guten Ergebnis entfernt ist, da zwischen den physikochemischen Parametern und den Reaktionswahrscheinlichkeiten keine linearen Zusammenhänge bestehen. Zudem müßten bei der Verwendung einer linearen
Regressionsanalyse die vorhergesagten Wahrscheinlichkeiten anschließend auf den Wertebereich von 0.0 bis 1.0 beschränkt werden, da nur solche Werte für eine Simulation geeignet sind.
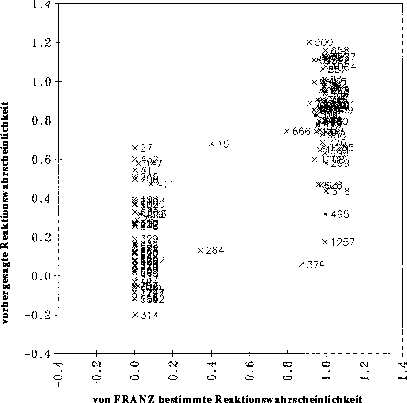
Abbildung 22: Diagramm, bei der die mit einer multilinearen Regression vorhergesagten Reaktionswahrscheinlichkeiten gegen die von FRANZ bestimmten (Sollwerte) aufgetragen sind. Nach manuellem Ausschluß falscher Datenpunkte: 115 Datenpunkte.
13
signifikante Variablen, Korrelationskoeffizient r = 0.8376
Da nur eine sehr geringe Anzahl von Datenpunkten eine mittlere Reaktivität besitzt, kann man auch an eine logistische Regressionsanalyse [40] denken, die zur Berechnung der Wahrscheinlichkeit nicht linear ist. Zuvor
wird allerdings, wie in der multilinearen Regression, eine Linearkombination der verwendeten Variablen gebildet.
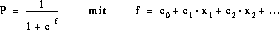
Betrachtet man das Diagramm in Abbildung 22 unter dem Aspekt, daß eine anschließende Funktion die vorhergesagten Reaktionswahrscheinlichkeiten oberhalb eines Schwellwerts in Richtung 1.0 und Werte unterhalb in Richtung
0.0 verschiebt, wie es bei der logistischen Regression durchgeführt wird, sind keine befriedigenden Ergebnisse zu erwarten, da die Linearkombination nicht in der Lage ist, die Datenpunkte richtig in zwei Gruppen zu trennen (siehe Abbildung
22).
Für Datensätze, bei denen weder die korrekten Datenpunkte noch die beschreibenden Variablen bekannt sind, wurde eine Technik entwickelt, die auch solche Daten behandeln kann [41][42].
Hierzu werden zwei verschiedene Typen neuronaler Netze verwendet. Kern dieser Methode ist, die Zahl der Variablen durch Reconstruction Learning [43], einem Backpropagationnetz [44]
mit modifiziertem Trainingsalgorithmus, und eventuell manuell durch chemisches Wissen soweit zu reduzieren, daß man anschließend mit einem Kohonennetz [45] falsch klassifizierte Datenpunkte als ähnliche
Datenpunkte mit deutlich abweichender Reaktionwahrscheinlichkeit erkennen und aus dem Datensatz entfernen kann. Kann nicht eindeutig entschieden werden, welcher Datenpunkt falsch bestimmt wurde, da etwa gleich viele ähnliche Datenpunkte mit hoher und niedriger
Reaktivität enthalten sind, werden all diese sich widersprechenden Datenpunkte gelöscht. Danach können durch das Reconstruction Learning die für die Beschreibung der Reaktivität relevanten Variablen herausgefunden werden, wobei mit
allen möglichen begonnen wird. Mit den so herausgefundenen Datenpunkten und Variablen wird nun das endgültige Backpropagationnetz trainiert, das auch nichtlineare Zusammenhänge beschreiben kann. Testet man nun die zuvor aus dem Datensatz herausgenommenen
Datenpunkte mit dem so gewonnenen Backpropagationnetz auf ihre Reproduktion, stellt man fest, daß nur etwa die Hälfte dieser Datenpunkte stark von den vorhergesagten Werten abweicht. Der Ablauf ist in Abbildung 23
zusammengefaßt.
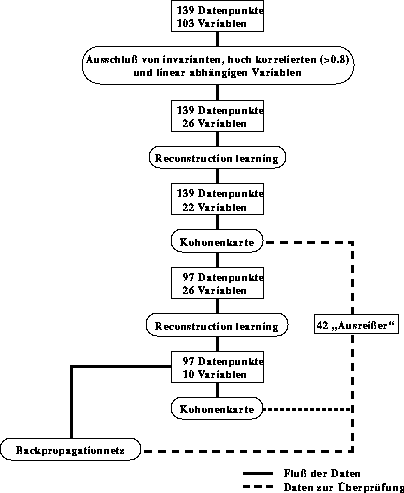
Abbildung 23: Beispiel des Ablaufschemas zum Training des Backpropagationnetzes.
Beim Training des Backpropagationnetzes muß noch darauf geachtet werden, daß dieses die Datenpunkte nicht auswendig lernt, sondern verallgemeinert. Man kann es dazu zwingen, indem man die Zahl der Gewichte, die von der Zahl der verwendeten Parameter,
der Zahl der versteckten Schichten (hidden layer) und der Zahl der Neuronen in ihnen abhängt, soweit reduziert, daß man etwa einen Faktor 3:1 für die Zahl der trainierten Datenpunkte zur Zahl der Gewichte im Netz oder besser noch größer
erhält. Ein höherer Faktor ist allerdings oft schwierig zu realisieren, da die Zahl der akkuraten Datenpunkte begrenzt ist.
Mit dieser Methode erhält man eine Gegenüberstellung der Sollwerte, die von FRANZ bestimmt wurden, und der vom Backpropagationnetz vorhergesagten wie in Abbildung 24. Das Backpropagationnetz wurde mit 97 Datenpunkten
und einem RMS-Wert (Route Mean Square) von 0.024 trainiert. Die Netzarchitektur sind 10 Eingabeneuronen (Variablen), eine versteckte Schicht mit 2 Neuronen und ein Ausgabeneuron, also ein Netz mit 25 Gewichten (inkl. BIAS, einem Neuron, das zur konstanten Verschiebung
der Summe der gewichteten Eingabewerte eines Neurons immer den Wert eins liefert.). Damit ist das Verhältnis Datenpunkte (97) zu Gewichten (25), wie gefordert, größer 3. Sagt man mit diesem Netz für alle 139 Datenpunkte, inklusive der 42
Ausreißer, die Reaktionswahrscheinlichkeiten vorher, erhält man nur für 32 Reaktionen Fehler der Reaktionswahrscheinlichkeit größer 0.3.

Abbildung 24: Diagramm, bei der die mit dem Backpropagationnetz vorhergesagten Reaktionswahrscheinlichkeiten für alle 139 Datenpunkte gegen die von FRANZ bestimmten (Sollwerte) aufgetragen sind.
Schließlich wird das so gewonnene Backpropagationnetz überprüft. Üblicherweise teilt man hierzu die Datenpunkte vor dem Training in einen Trainings- und Testdatensatz. Die Datenpunkte im Testdatensatz werden nach dem Training verwendet,
um die Güte des Netzes festzustellen. In einigen Fällen, wie auch für die Vorhersage der Reaktionswahrscheinlichkeiten für die Carbonyleliminierung, reichen die Datenpunkte hierzu jedoch nicht aus. Ist die Gewinnung zusätzlicher Datenpunkte
nur schwer möglich, muß eine andere Methode gefunden werden, das Netz zu testen. Im Fall der Carbonyleliminierung wurden die von FRANZ bewerteten Reaktionen in zwei Klassen eingeteilt (siehe 4.2.2.2): diejenigen,
bei denen die Differenz der Unter- und Obergrenze für die Reaktionswahrscheinlichkeiten den Wert 0.2 (Klasse-1) bzw. 0.4 (Klasse-2) nicht überschreiten. Für die Ableitung des neuronalen Netzes wurden alle 139 Carbonyleliminierungen der Klasse-1
verwendet. Zur Überprüfung können die 224 etwas unsichereren Datenpunkte der Klasse-2 eingesetzt werden. Besonderer Wert bei dieser Überprüfung muß dabei auf zusätzliche Datenpunkte in der Klasse-2 gelegt werden, da die Klasse-2
auch alle Datenpunkte der Klasse-1 enthält, die für die Ableitung des Netzes verwendet wurde. Die Datenpunkte, die sowohl in der Klasse-1, als auch in der Klasse-2 enthalten sind, können für die beiden Klassen von FRANZ unterschiedliche
Werte zugeordnet bekommen. Ein Datenpunkt entspricht einer Reaktion, die FRANZ bei der Analyse der untersuchten Massenspektren und Strukturen öfters gefunden haben kann. Tritt eine bestimmte Reaktion mehrmals auf, trägt FRANZ den Mittelwert der aufgetretenen
Reaktionswahrscheinlichkeiten in der Datenbank der Reaktionen unter der entsprechenden Klasse ein. Dies ist beispielsweise für die Reaktion 732 zu beobachten: Klasse-1 0.915; vorhergesagter Wert 0.893; Klasse-2 0.793.
Überprüft man nun das Backpropagationnetz mit den Datenpunkten der Klasse-2, haben 53 der 224 Datenpunkte eine Abweichung der Reaktionswahrscheinlichkeit größer 0.3 (siehe Abbildung 25). Vergleicht man
diesen Anteil abweichender Reaktionswahrscheinlichkeiten für Datenpunkte der Klasse-2 mit denen der Klasse-1 (32 aus 139 mit einer Abweichung größer 0.3), stellt man fest, daß bei fast doppelter Anzahl der Datenpunkte der Prozentsatz nahezu
identisch ist. Zusammenfassend kann man sagen, daß das Backpropagationnetz für die Schwierigkeiten ein brauchbares Ergebnis liefert.

Abbildung 25: Diagramm der Klasse-2-Datenpunkte gegen die von FRANZ bestimmten Werte.
Schafft man es so für alle Reaktionstypen neuronale Netze zu trainieren und für die Umlagerungsreaktionen logistische Regressionsanalysen bzw. auch ein Backpropagationnetz zu trainieren, hat man bei einer Simulation, die die gewonnenen Reaktivitätsfunktionen"
verwenden, immer noch die Probleme, daß für konkurrierende Reaktionen aus Umlagerungssystemen oft nicht, wie notwendig, unterschiedliche Reaktionswahrscheinlichkeiten vorhergesagt werden können (siehe 4.2.2.3).
4.2.5.2. Regeln ohne Umlagerungsreaktionstypen
Für die Ableitung der neuronalen Netze zur Bewertung der einzelnen Reaktionen unter Ausschluß von Umlagerungsreaktionstypen wurden die Fragmentierungstypen, wie in Kapitel 4.2.3.2 beschrieben, verwendet. Der gesamte
Satz an Reaktionstypen ist in Abbildung 26 gezeigt.
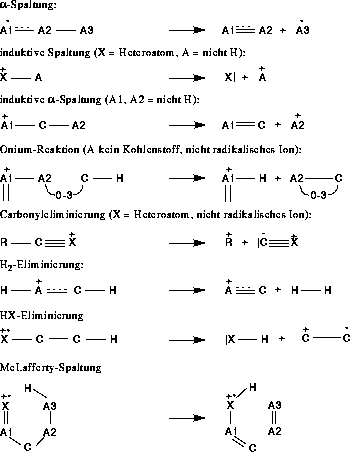
Abbildung 26: Regeln ohne Umlagerungsreaktionstypen.
Als Daten wurden die Strukturen und Massenspektren von 103 Moleküle genommen, die alle nur eine funktionelle Gruppe und keine Ringe enthalten. Ringe wurden ausgeschlossen, damit auch Fragmentierungsreaktionstypen keine Umlagerungsreaktionen erzeugen, indem
eine der Ringbindungen gebrochen wird. Die Moleküle dieses Datensatzes sind in Anhang C gezeigt und enthält:
6 Carbonsäuren
19 Ester (8 kurzkettige und 11 langkettige)
1 Amid
7 Aldehyde
5 Ketone
8 Acetale
2 Ketale
6 Ether
1 Thioether
1 Thiol
10 Alkohole (4 primär, 4 sekundär und 2 tertiär)
15 Amine (5 primär, 4 sekundär und 6 tertiär)
12 Halogenide (6 Chloride, 4 Bromide und 2 Iodide)
10 Alkene
Die Summe aller Signalintensitäten in den Massenspektren dieser Verbindungen konnte von FRANZ durchschnittlich zu 73% aufgeklärt werden. Die so erzeugten Reaktionsdatenbanken mit Reaktionswahrscheinlichkeiten wurden anschließend in gleicher Weise
für die Ableitung der neuronalen Netze bzw. der expliziten Funktionen eingesetzt, wie es in 4.2.5.1 beschrieben ist (Regeln mit Umlagerungstypen). Um zu zeigen, daß so Massenspektren vorhergesagt werden können,
wurden zunächst nur Bewertungen für folgende vier Fragmentierungstypen abgeleitet:  -Spaltung, Oniumspaltung, Carbonyleliminierung und die McLafferty-Spaltung (siehe Abbildung 27). Die Beschränkungen
auf nur eine funktionelle Gruppe, keine Ringe und auf vier bewertete Fragmentierungstypen begrenzt die Einsatzmöglichkeit der so gewonnenen Regeln für die Simulation von Spektren durch das Programm MASSIMO auf Verbindungen, in deren Massenspektren
keine anderen Fragmentierungstypen eine entscheidende Rolle spielen und bei denen die Fragmentierung einer funktionellen Gruppe nicht durch die Anwesenheit einer anderen beeinflußt wird.
-Spaltung, Oniumspaltung, Carbonyleliminierung und die McLafferty-Spaltung (siehe Abbildung 27). Die Beschränkungen
auf nur eine funktionelle Gruppe, keine Ringe und auf vier bewertete Fragmentierungstypen begrenzt die Einsatzmöglichkeit der so gewonnenen Regeln für die Simulation von Spektren durch das Programm MASSIMO auf Verbindungen, in deren Massenspektren
keine anderen Fragmentierungstypen eine entscheidende Rolle spielen und bei denen die Fragmentierung einer funktionellen Gruppe nicht durch die Anwesenheit einer anderen beeinflußt wird.
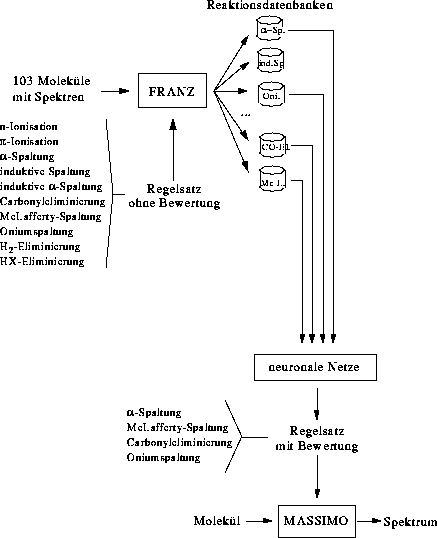
Abbildung 27: Ableitung der Bewertungen für die vier Fragmentierungstypen  -Spaltung, McLafferty-Spaltung, Carbonyleliminierung und Oniumspaltung.
-Spaltung, McLafferty-Spaltung, Carbonyleliminierung und Oniumspaltung.
Für die drei Fragmentierungstypen  -Spaltung, Oniumreaktion und Carbonyleliminierung wurden jeweils Backpropagationnetze ausgehend von den Datenpunkten in den Reaktionsdatenbanken der Klasse-1 trainiert. Die Reaktionen der Klasse-1
sind für die
-Spaltung, Oniumreaktion und Carbonyleliminierung wurden jeweils Backpropagationnetze ausgehend von den Datenpunkten in den Reaktionsdatenbanken der Klasse-1 trainiert. Die Reaktionen der Klasse-1
sind für die  -Spaltung in Anhang D.2.1, für die Oniumreaktion in Anhang D.2.2 und für die Carbonyleliminierung in Anhang D.2.3
gezeigt.
-Spaltung in Anhang D.2.1, für die Oniumreaktion in Anhang D.2.2 und für die Carbonyleliminierung in Anhang D.2.3
gezeigt.
Ausgehend von 153 Datenpunkten der Klasse-1 konnte nach dem Ausschluß der Ausreißer" und damit der Reduktion der Datenpunkte auf 126 ein Backpropagationnetz abgeleitet werden [41], das die Reaktionswahrscheinlichkeiten
der  -Spaltung aus 12 Variablen vorhersagt. Das Netz besitzt neben den 12 Eingabeneuronen eine versteckte Schicht aus drei Neuronen und ein Ausgabeneuron. Zählt man das BIAS-Neuron mit, das immer den Wert 1.0 liefert und somit
den Übergangsbereich der sigmoiden Transferfunktion auf das Neuron in der nächsten Schicht verschiebt, besitzt dieses Netz 43 Gewichte. Es ist in Abbildung 28 dargestellt und hatte nach dem Training für die
126 Datenpunkte einen RMS-Wert von 0.095. 37 Werte hatten bei der Vorhersage eine Abweichung größer 0.1, vier größer 0.2 und ein Wert größer als 0.3. Kein Wert hatte eine Abweichung größer 0.4.
-Spaltung aus 12 Variablen vorhersagt. Das Netz besitzt neben den 12 Eingabeneuronen eine versteckte Schicht aus drei Neuronen und ein Ausgabeneuron. Zählt man das BIAS-Neuron mit, das immer den Wert 1.0 liefert und somit
den Übergangsbereich der sigmoiden Transferfunktion auf das Neuron in der nächsten Schicht verschiebt, besitzt dieses Netz 43 Gewichte. Es ist in Abbildung 28 dargestellt und hatte nach dem Training für die
126 Datenpunkte einen RMS-Wert von 0.095. 37 Werte hatten bei der Vorhersage eine Abweichung größer 0.1, vier größer 0.2 und ein Wert größer als 0.3. Kein Wert hatte eine Abweichung größer 0.4.
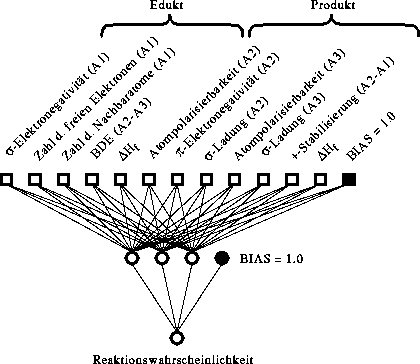
Abbildung 28: Aufbau des Backpropagationnetzes zur Vorhersage der Reaktionswahrscheinlichkeit der  -Spaltung.
-Spaltung.
Die Reproduktionsfähigkeit der Reaktionswahrscheinlichkeiten dieses Netzes ist in Abbildung 29 gezeigt. Hier sind die vorhergesagten gegen die von FRANZ vorgegebenen Wahrscheinlichkeiten aller 153 Klasse-1-Daten aufgetragen.
Diesem Diagramm ist zu entnehmen, daß die Zusammenhänge vom Backpropagationnetz erkannt wurden und auch größtenteils reproduziert werden können. Die Zahl der Punkte der Reaktionen mit einer starken Abweichung der vorhergesagten Wahrscheinlichkeit
deuten darauf hin, daß dem Netz nicht alle notwendigen Informationen zur Verfügung stehen. Dazu gehört sicherlich die Spezifikation der Anregungsenergie des Kations, die stark von seiner Entstehungsgeschichte abhängt. Die Energieverteilung
der Ionen ändert sich einerseits mit der Reaktionsenthalpie, wenn das Ion genügend Energie besitzt, um die Aktivierungsbarriere zu überwinden. Wird bei der Fragmentierung ein Neutralfragment abgespalten, verliert das Kation um so mehr Energie,
je größer und schwerer das abgespaltene Molekül ist. Da im Massenspektrometer bevorzugt große Fragmente abgespalten werden, verliert das Kation bei solchen Reaktionen den größten Teil seiner Anregungsenergie. Die Reaktionswahrscheinlichkeit
dieser kalten Ionen muß wesentlich kleiner sein als die von Kationen mit einer Anregungsenergie, wie sie nach einer Elektronenstoßionisation vorliegt.
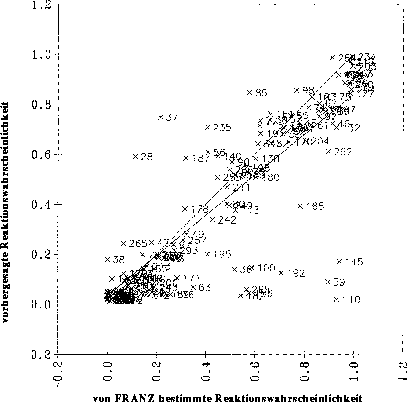
Abbildung 29: Korrelation der vom Backpropagationnetz vorhergesagten mit den von FRANZ ermittelten Reaktionswahrscheinlichkeiten für die  -Spaltung. Die durchgezogene Linie ist die Regressionsgerade und die gestrichelte
die Winkelhalbierende, auf der alle Punkte idealerweise liegen sollten. Die Nummern der Datenpunkte sind die Nummern der Reaktionen im Anhang D.2.1.
-Spaltung. Die durchgezogene Linie ist die Regressionsgerade und die gestrichelte
die Winkelhalbierende, auf der alle Punkte idealerweise liegen sollten. Die Nummern der Datenpunkte sind die Nummern der Reaktionen im Anhang D.2.1.
Auch für die Oniumreaktion wurde mit 44 von 49 Klasse-1-Daten ein Backpropagationnetz trainiert, das 11 Variablen verwendet und zwei Neuronen in einer versteckten Schicht besitzt. Der RMS-Wert betrug 0.061, aber mit 27 Gewichten bei 44 Datenpunkten genügt
es dem Kriterium, daß die Zahl der Datenpunkte mehr als dreimal so groß sein soll, wie die Zahl der Gewichte im Netz, nicht. Da eine weitere Reduktion der Variablen und damit der Gewichte ohne drastischen Verlust an Reproduktionsfähigkeit der
trainierten Daten nicht möglich war und nicht so einfach zusätzlich Datenpunkte beschafft werden konnten, wurde das Netz dennoch für die Simulation herangezogen. Daß dieses Netz auch für andere Reaktionen, die nicht trainiert wurden,
die Reaktionswahrscheinlichkeiten korrekt vorhersagen kann, ist nicht unbedingt anzunehmen, da es bei diesem Verhältnis Datenpunkte zu Gewichten im Netz durchaus möglich ist, daß einige Datenpunkte vom Netz auswendig gelernt wurden und nicht
überall der Zusammenhang verallgemeinert wurde. Die Korrelation der von diesem Netz vorhergesagten Datenpunkte der Klasse-1 der Oniumreaktionen ist in Abbildung 30 zu sehen.
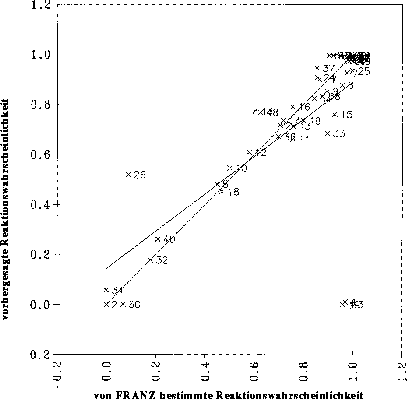
Abbildung 30: Korrelation der vom Backpropagationnetz vorhergesagten mit den von FRANZ ermittelten Reaktionswahrscheinlichkeiten für die Oniumreaktion. Die durchgezogene Linie ist die Regressionsgerade und die gestrichelte die Winkelhalbierende,
auf der alle Punkte idealerweise liegen sollten. Die Nummern der Datenpunkte sind die Nummern der Reaktionen im Anhang D.2.2.
Noch schlechter war die Situation mit 13 Datenpunkten der Klasse-1 für die Carbonyleliminierung. Trainiert wurde ein Backpropagationnetz mit 11 der 13 Datenpunkte, 2 Variablen und einem Neuron in einer versteckten Schicht und einem RMS-Wert von 0.128.
Abbildung 31 zeigt die Gegenüberstellung der vorhergesagten und der vorgegebenen Werte.
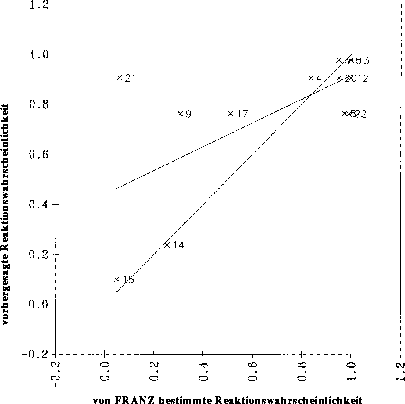
Abbildung 31: Korrelation der vom Backpropagationnetz vorhergesagten mit den von FRANZ ermittelten Reaktionswahrscheinlichkeiten für die Carbonyleliminierung. Die durchgezogene Linie ist die Regressionsgerade und die gestrichelte die Winkelhalbierende,
auf der alle Punkte idealerweise liegen sollten. Die Nummern der Datenpunkte sind die Nummern der Reaktionen im Anhang D.2.3.
Für die McLafferty-Spaltung gab es schließlich nur noch vier Datenpunkte in der Klasse-1. Deshalb wurden alle 14 Datenpunkte der Klasse-2 (siehe Anhang D.2.4) herangezogen. Betrachtet man sich den Datensatz genauer,
fällt auf, daß sich die McLafferty-Reaktionen in zwei Gruppen teilen. Zehn Reaktionen mit Reaktionswahrscheinlichkeiten von 0.787 bis 0.894 bilden eine Gruppe, bei denen das Wasserstoffatom von einer CH2-Gruppe auf das Carbonylsauerstoffatom umgelagert
wird. Die andere Gruppe sind vier Reaktionen, bei denen das Wasserstoffatom von einer Methylgruppe abgezogen wird und Wahrscheinlichkeiten von 0.002 bis 0.544 haben. Demzufolge erhalten die McLafferty-Reaktionen die Mittelwerte der Reaktionswahrscheinlichkeiten
0.8361 (H von CH2) bzw. 0.23 (H von CH3).
![[Prev]](p_prev.gif)
![[Next]](p_next.gif)
robert(at)robert-hoellering.de
Copyright © 1998, Höllering Universität Erlangen-Nürnberg. All rights
reserved.
![[Prev]](p_prev.gif)
![[Next]](p_next.gif)
![[Prev]](p_prev.gif)
![[Next]](p_next.gif)
 -Ionisation. Angaben wie 3-7 besagen, daß an dieser Stelle eine Kette von
Atomen einer Länge zwischen drei und sieben ist. Dies ist der Satz aller möglichen Reaktionstypen. Welche Reaktionen auch tatsächlich im Massenspektrometer stattfinden und in welchem Ausmaß, wird von FRANZ (Fragmentation and Rearrangement
ANalyZer) aus den Reaktionstypen, dem experimentellen Massenspektrum und der Struktur der Verbindung ermittelt [23][24]. Ergebnis der Berechnungen von FRANZ sind dann Datenbanken
für die einzelnen Reaktionstypen mit Reaktionen diesen Typs, denen eine Reaktionswahrscheinlichkeit zugeordnet ist.
-Ionisation. Angaben wie 3-7 besagen, daß an dieser Stelle eine Kette von
Atomen einer Länge zwischen drei und sieben ist. Dies ist der Satz aller möglichen Reaktionstypen. Welche Reaktionen auch tatsächlich im Massenspektrometer stattfinden und in welchem Ausmaß, wird von FRANZ (Fragmentation and Rearrangement
ANalyZer) aus den Reaktionstypen, dem experimentellen Massenspektrum und der Struktur der Verbindung ermittelt [23][24]. Ergebnis der Berechnungen von FRANZ sind dann Datenbanken
für die einzelnen Reaktionstypen mit Reaktionen diesen Typs, denen eine Reaktionswahrscheinlichkeit zugeordnet ist.

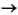 B und A
B und A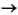 C um den Teil, der der
im Spektrum sichtbaren Fragmente B und C entspricht. Für reaktive Reaktionen mit einer Wahrscheinlichkeit größer ca. 0.7 hat dies zur Folge, daß über diese Reaktion eigentlich keine sichere Aussage für die Reaktionswahrscheinlichkeit
mehr getroffen werden kann, da sie zwischen 0.0 und 0.7 bzw. noch höher liegen, also fast alle Wahrscheinlichkeitswerte besitzen kann.
C um den Teil, der der
im Spektrum sichtbaren Fragmente B und C entspricht. Für reaktive Reaktionen mit einer Wahrscheinlichkeit größer ca. 0.7 hat dies zur Folge, daß über diese Reaktion eigentlich keine sichere Aussage für die Reaktionswahrscheinlichkeit
mehr getroffen werden kann, da sie zwischen 0.0 und 0.7 bzw. noch höher liegen, also fast alle Wahrscheinlichkeitswerte besitzen kann.  -Spaltungen betrachtet, die von zwei verschiedenen Fragmenten eines Umlagerungssystems ausgehen. Diese Reaktionen finden beispielsweise im Massenspektrometer bei der Aufnahme der Spektren
von Fettsäuren und deren Estern statt. Abbildung 9 zeigt hierfür ein Beispiel, wobei der unterlegte Teil das nur teilweise gezeigte Umlagerungssystem darstellt. Die Reaktionen unten sind die konkurrierenden
-Spaltungen betrachtet, die von zwei verschiedenen Fragmenten eines Umlagerungssystems ausgehen. Diese Reaktionen finden beispielsweise im Massenspektrometer bei der Aufnahme der Spektren
von Fettsäuren und deren Estern statt. Abbildung 9 zeigt hierfür ein Beispiel, wobei der unterlegte Teil das nur teilweise gezeigte Umlagerungssystem darstellt. Die Reaktionen unten sind die konkurrierenden  -Spaltungen.
-Spaltungen.
 -Spaltungen aus einem Umlagerungssystem.
-Spaltungen aus einem Umlagerungssystem. -Spaltung (m/z 129) etwa in doppelt bis dreimal so großem Ausmaß gebildet wird wie das linke (m/z 115) (siehe Abbildung 10), kann
sicherlich nicht an den unterschiedlich stark ablaufenden
-Spaltung (m/z 129) etwa in doppelt bis dreimal so großem Ausmaß gebildet wird wie das linke (m/z 115) (siehe Abbildung 10), kann
sicherlich nicht an den unterschiedlich stark ablaufenden  -Spaltungen liegen, da die elektronischen und energetischen Verhältnisse vergleichbar sind. Da FRANZ das Umlagerungssystem zusammenfaßt und nur eine Konzentration
dafür besitzt, verwendet FRANZ diese Konzentration auch als Eduktkonzentration für die Berechnung der Reaktionswahrscheinlichkeiten. Die unterschiedlichen Produkt- und gleichen Eduktkonzentrationen haben verschiedene Reaktionswahrscheinlichkeiten
zur Folge. Dies kann man allerdings nicht, wie oben gesagt wurde, durch die Verhältnisse am Reaktionszentrum erklären. Die unterschiedliche Bildung der Produkte der
-Spaltungen liegen, da die elektronischen und energetischen Verhältnisse vergleichbar sind. Da FRANZ das Umlagerungssystem zusammenfaßt und nur eine Konzentration
dafür besitzt, verwendet FRANZ diese Konzentration auch als Eduktkonzentration für die Berechnung der Reaktionswahrscheinlichkeiten. Die unterschiedlichen Produkt- und gleichen Eduktkonzentrationen haben verschiedene Reaktionswahrscheinlichkeiten
zur Folge. Dies kann man allerdings nicht, wie oben gesagt wurde, durch die Verhältnisse am Reaktionszentrum erklären. Die unterschiedliche Bildung der Produkte der  -Spaltungen liegt vielmehr daran, daß die Wasserstoffumlagerungen
mit unterschiedlichen Reaktivitäten ablaufen und daher zu unterschiedlichen Konzentrationen für die Edukte der nachfolgenden
-Spaltungen liegt vielmehr daran, daß die Wasserstoffumlagerungen
mit unterschiedlichen Reaktivitäten ablaufen und daher zu unterschiedlichen Konzentrationen für die Edukte der nachfolgenden  -Spaltungen führen. Dies kann auch dadurch belegt werden, daß das Signalmuster eines
Fettsäureesters gut reproduziert werden kann (siehe Abbildung 10), wenn ausgehend von den Molekülionen zu 10% eine
-Spaltungen führen. Dies kann auch dadurch belegt werden, daß das Signalmuster eines
Fettsäureesters gut reproduziert werden kann (siehe Abbildung 10), wenn ausgehend von den Molekülionen zu 10% eine  -Spaltung stattfindet und die restlichen 90% eine Wasserstoffumlagerung
eingehen, wobei diese zu 15% über einen 5-, zu 80% über einen 6- und zu 5% über einen 7-gliedrigen Übergangszustand erfolgt und bei allen
-Spaltung stattfindet und die restlichen 90% eine Wasserstoffumlagerung
eingehen, wobei diese zu 15% über einen 5-, zu 80% über einen 6- und zu 5% über einen 7-gliedrigen Übergangszustand erfolgt und bei allen  -Spaltungen ein Alkylradikal abgespalten wird. [47]
-Spaltungen ein Alkylradikal abgespalten wird. [47]
 -Spaltungen gebildet werden, mit dem experimentellen
Massenspektrum [22] von Methylstearat.
-Spaltungen gebildet werden, mit dem experimentellen
Massenspektrum [22] von Methylstearat. 
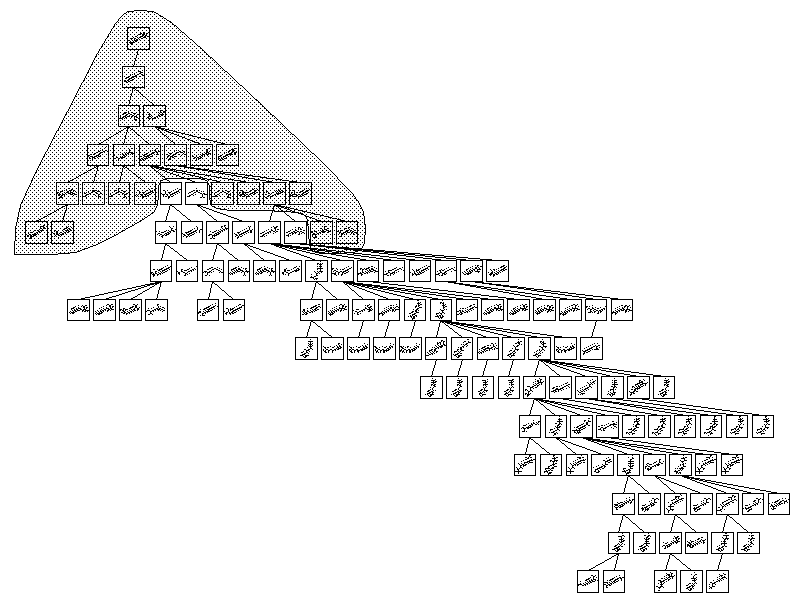
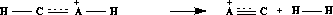
 O+-Ions und aller seiner Folgeprodukte, der Serie der Alkylfragmente,
gefunden werden, wurde diese Reaktion ausgeschlossen, wenn das Radikalzentrum und die positive Ladung an einem Atom lokalisiert sind (siehe Abbildung 14). Ohne diesen Ausschluß könnten die
O+-Ions und aller seiner Folgeprodukte, der Serie der Alkylfragmente,
gefunden werden, wurde diese Reaktion ausgeschlossen, wenn das Radikalzentrum und die positive Ladung an einem Atom lokalisiert sind (siehe Abbildung 14). Ohne diesen Ausschluß könnten die  -Spaltung
(Abspaltung eines Wasserstoffradikals) und die Eliminierung von Wasserstoffmolekülen in beiden Reihenfolgen auf das Molekülion angewendet werden, wobei das R-C
-Spaltung
(Abspaltung eines Wasserstoffradikals) und die Eliminierung von Wasserstoffmolekülen in beiden Reihenfolgen auf das Molekülion angewendet werden, wobei das R-C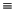 O+-Ion entsteht, und FRANZ könnte für die Reaktionen
keine sicheren Reaktionswahrscheinlichkeiten berechnen (siehe 4.2.2.2).
O+-Ion entsteht, und FRANZ könnte für die Reaktionen
keine sicheren Reaktionswahrscheinlichkeiten berechnen (siehe 4.2.2.2).



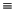 O+-Ion spaltet Kohlenmonoxid ab und fragmentiert danach wie Alkylkationen. Dazu wird der Reaktionstyp der induktiven
O+-Ion spaltet Kohlenmonoxid ab und fragmentiert danach wie Alkylkationen. Dazu wird der Reaktionstyp der induktiven  -Spaltung benötigt [27],
der ebenfalls neu eingeführt wurde.
-Spaltung benötigt [27],
der ebenfalls neu eingeführt wurde.
 -Spaltung.
-Spaltung.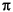 -Ionisation, sowie die
-Ionisation, sowie die  -Spaltung und die Oniumspaltung blieben unverändert. Der sich daraus ergebende Regelsatz ist in Abbildung 19 gezeigt.
-Spaltung und die Oniumspaltung blieben unverändert. Der sich daraus ergebende Regelsatz ist in Abbildung 19 gezeigt.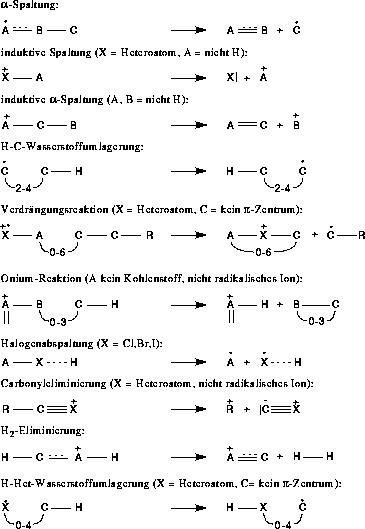
 -Spaltung darstellt, und der HX-Eliminierung eingeführt, hinter der sich die Wasserstoffumlagerung mit nachgeschalteter induktiver Spaltung verbirgt. Diese beiden Reaktionstypen sind in Abbildung
20 dargestellt. X ist ein Heteroatom.
-Spaltung darstellt, und der HX-Eliminierung eingeführt, hinter der sich die Wasserstoffumlagerung mit nachgeschalteter induktiver Spaltung verbirgt. Diese beiden Reaktionstypen sind in Abbildung
20 dargestellt. X ist ein Heteroatom.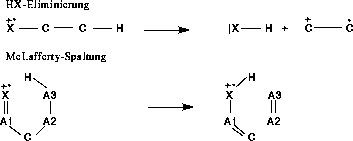
 -Spaltung und die induktive Spaltung auch für
die Halogenide gültig sind. Dies hat zur Folge, daß einige Signale für die halogenhaltigen Substanzen von FRANZ nicht erklärt werden können, aber die durchgeführten Reaktionen werden richtig bewertet, wenn, wie im Fall der Verdrängungsreaktionen,
die Folgereaktionen nur von geringer Bedeutung sind oder, wie im Fall der Halogenspaltung, die Reaktionen nur vernachlässigbare Umsätze besitzen, da im Datensatz nur Monohalogenide enthalten sind.
-Spaltung und die induktive Spaltung auch für
die Halogenide gültig sind. Dies hat zur Folge, daß einige Signale für die halogenhaltigen Substanzen von FRANZ nicht erklärt werden können, aber die durchgeführten Reaktionen werden richtig bewertet, wenn, wie im Fall der Verdrängungsreaktionen,
die Folgereaktionen nur von geringer Bedeutung sind oder, wie im Fall der Halogenspaltung, die Reaktionen nur vernachlässigbare Umsätze besitzen, da im Datensatz nur Monohalogenide enthalten sind.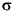 -Partialladungen und
-Partialladungen und 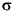 -Restelektronegativitäten der Atome [29][30]. Die Verteilung der
Elektronen in
-Restelektronegativitäten der Atome [29][30]. Die Verteilung der
Elektronen in 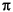 -Systemen basiert auf dem Konzept der Orbitalelektronegativitäten [31].
-Systemen basiert auf dem Konzept der Orbitalelektronegativitäten [31].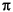 -Systeme und freie Elektronenpaare
enthalten. Hier gibt es Schwierigkeiten zu erkennen, welche Elektronensysteme miteinander konjugiert sind und welche nicht. Zusätzlich kann in der Bindungsliste in solchen Fällen oft nicht eindeutig ein bestimmtes Elektronensystem spezifiziert werden,
aus dem bei der Ionisation das Elektron entfernt wurde. Für die übrigen Verbindungen liegen die Abweichungen von den experimentellen Werten etwa in der Größenordnung der Meßgenauigkeit. Zur Vermeidung dieser Abweichungen ist eine Verbesserung
der Darstellung der chemischen Struktur sowie eine Neugestaltung des Algorithmus für die Berechnung erforderlich. Als Beispiel hierfür dienen ionisierte, ungesättigte Verbindungen, bei denen ein freies Elektronenpaar mit dem
-Systeme und freie Elektronenpaare
enthalten. Hier gibt es Schwierigkeiten zu erkennen, welche Elektronensysteme miteinander konjugiert sind und welche nicht. Zusätzlich kann in der Bindungsliste in solchen Fällen oft nicht eindeutig ein bestimmtes Elektronensystem spezifiziert werden,
aus dem bei der Ionisation das Elektron entfernt wurde. Für die übrigen Verbindungen liegen die Abweichungen von den experimentellen Werten etwa in der Größenordnung der Meßgenauigkeit. Zur Vermeidung dieser Abweichungen ist eine Verbesserung
der Darstellung der chemischen Struktur sowie eine Neugestaltung des Algorithmus für die Berechnung erforderlich. Als Beispiel hierfür dienen ionisierte, ungesättigte Verbindungen, bei denen ein freies Elektronenpaar mit dem 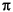 -System
(teilweise) konjugiert ist, wie bei den Jodtoluolen, Brombenzol oder 1,1-Difluorethen. Aber auch bei ionisierten Chinonen treten bei bestimmten mesomeren Grenzstrukturen starke Abweichungen auf. Für diese Substanzen sind Differenzen bei der Bildungswärme
von ca. 200 bis 600 kJ/mol zu beobachten. Legt man der Berechnung der Bildungswärmen eine chemische Datenstruktur zugrunde, bei der die Konjugation von Doppel- und Dreifachbindungen sowie von freien Elektronenpaaren Bestandteil der chemischen Datenstruktur
ist, müßten diese Probleme bewältigt werden können. Aus der Differenz der Bildungswärmen der Produkte und Edukte läßt sich auch die Reaktionsenthalpie berechnen.
-System
(teilweise) konjugiert ist, wie bei den Jodtoluolen, Brombenzol oder 1,1-Difluorethen. Aber auch bei ionisierten Chinonen treten bei bestimmten mesomeren Grenzstrukturen starke Abweichungen auf. Für diese Substanzen sind Differenzen bei der Bildungswärme
von ca. 200 bis 600 kJ/mol zu beobachten. Legt man der Berechnung der Bildungswärmen eine chemische Datenstruktur zugrunde, bei der die Konjugation von Doppel- und Dreifachbindungen sowie von freien Elektronenpaaren Bestandteil der chemischen Datenstruktur
ist, müßten diese Probleme bewältigt werden können. Aus der Differenz der Bildungswärmen der Produkte und Edukte läßt sich auch die Reaktionsenthalpie berechnen.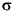 -Elektronegativitäten zweier
benachbarter Atome im Reaktionszentrum und die
-Elektronegativitäten zweier
benachbarter Atome im Reaktionszentrum und die 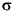 -Elektronegativitäten dieser Atome.
-Elektronegativitäten dieser Atome.





 -Spaltung, Oniumspaltung, Carbonyleliminierung und die McLafferty-Spaltung (siehe Abbildung 27). Die Beschränkungen
auf nur eine funktionelle Gruppe, keine Ringe und auf vier bewertete Fragmentierungstypen begrenzt die Einsatzmöglichkeit der so gewonnenen Regeln für die Simulation von Spektren durch das Programm MASSIMO auf Verbindungen, in deren Massenspektren
keine anderen Fragmentierungstypen eine entscheidende Rolle spielen und bei denen die Fragmentierung einer funktionellen Gruppe nicht durch die Anwesenheit einer anderen beeinflußt wird.
-Spaltung, Oniumspaltung, Carbonyleliminierung und die McLafferty-Spaltung (siehe Abbildung 27). Die Beschränkungen
auf nur eine funktionelle Gruppe, keine Ringe und auf vier bewertete Fragmentierungstypen begrenzt die Einsatzmöglichkeit der so gewonnenen Regeln für die Simulation von Spektren durch das Programm MASSIMO auf Verbindungen, in deren Massenspektren
keine anderen Fragmentierungstypen eine entscheidende Rolle spielen und bei denen die Fragmentierung einer funktionellen Gruppe nicht durch die Anwesenheit einer anderen beeinflußt wird.
 -Spaltung, McLafferty-Spaltung, Carbonyleliminierung und Oniumspaltung.
-Spaltung, McLafferty-Spaltung, Carbonyleliminierung und Oniumspaltung. -Spaltung, Oniumreaktion und Carbonyleliminierung wurden jeweils Backpropagationnetze ausgehend von den Datenpunkten in den Reaktionsdatenbanken der Klasse-1 trainiert. Die Reaktionen der Klasse-1
sind für die
-Spaltung, Oniumreaktion und Carbonyleliminierung wurden jeweils Backpropagationnetze ausgehend von den Datenpunkten in den Reaktionsdatenbanken der Klasse-1 trainiert. Die Reaktionen der Klasse-1
sind für die  -Spaltung in Anhang D.2.1, für die Oniumreaktion in Anhang D.2.2 und für die Carbonyleliminierung in Anhang D.2.3
gezeigt.
-Spaltung in Anhang D.2.1, für die Oniumreaktion in Anhang D.2.2 und für die Carbonyleliminierung in Anhang D.2.3
gezeigt.  -Spaltung aus 12 Variablen vorhersagt. Das Netz besitzt neben den 12 Eingabeneuronen eine versteckte Schicht aus drei Neuronen und ein Ausgabeneuron. Zählt man das BIAS-Neuron mit, das immer den Wert 1.0 liefert und somit
den Übergangsbereich der sigmoiden Transferfunktion auf das Neuron in der nächsten Schicht verschiebt, besitzt dieses Netz 43 Gewichte. Es ist in Abbildung 28 dargestellt und hatte nach dem Training für die
126 Datenpunkte einen RMS-Wert von 0.095. 37 Werte hatten bei der Vorhersage eine Abweichung größer 0.1, vier größer 0.2 und ein Wert größer als 0.3. Kein Wert hatte eine Abweichung größer 0.4.
-Spaltung aus 12 Variablen vorhersagt. Das Netz besitzt neben den 12 Eingabeneuronen eine versteckte Schicht aus drei Neuronen und ein Ausgabeneuron. Zählt man das BIAS-Neuron mit, das immer den Wert 1.0 liefert und somit
den Übergangsbereich der sigmoiden Transferfunktion auf das Neuron in der nächsten Schicht verschiebt, besitzt dieses Netz 43 Gewichte. Es ist in Abbildung 28 dargestellt und hatte nach dem Training für die
126 Datenpunkte einen RMS-Wert von 0.095. 37 Werte hatten bei der Vorhersage eine Abweichung größer 0.1, vier größer 0.2 und ein Wert größer als 0.3. Kein Wert hatte eine Abweichung größer 0.4.
 -Spaltung.
-Spaltung.
 -Spaltung. Die durchgezogene Linie ist die Regressionsgerade und die gestrichelte
die Winkelhalbierende, auf der alle Punkte idealerweise liegen sollten. Die Nummern der Datenpunkte sind die Nummern der Reaktionen im Anhang D.2.1.
-Spaltung. Die durchgezogene Linie ist die Regressionsgerade und die gestrichelte
die Winkelhalbierende, auf der alle Punkte idealerweise liegen sollten. Die Nummern der Datenpunkte sind die Nummern der Reaktionen im Anhang D.2.1.

![[Prev]](p_prev.gif)
![[Next]](p_next.gif)