7.1.3. Abbau von Umweltchemikalien

Beim Abbau von Umweltchemikalien handelt es sich vorwiegend um Reaktionen pseudoerster Ordnung. Von T. Kostka [62] wurden Regeln entwickelt, die den Abbau von s-Triazinen, die zu den Herbiziden gehören, durch reduktive Dealkylierung und Hydrolyse simulieren. Ein Beispiel hierfür wurde mit dem Abbau von Atrazin bereits im Kapitel 6.9.1 gezeigt. Ein weiteres Beispiel für den Abbau von s-Triazinen ist Prometon.

7.1.3.1. Abbau von Prometon

Für den Abbau von Umweltchemikalien durch Reaktionen pseudoerster Ordnung setzt man einen Reaktor mit einer Phase im Modus monomolekular" ein. Wird die Chemikalie, wie bei den s-Triazinen, zu einer bestimmten Zeit ausgebracht (nicht ständig), wird für sie eine Anfangskonzentration angegeben, aber kein kontinuierlicher Zufluß. Als Reaktionstypen werden die reduktive Dealkylierung und die Hydrolyse eingesetzt, die die im Überschuß vorliegenden Reaktionspartner Wasser und den formal für Reduktionsäquivalente verwendeten Wasserstoff während der Reaktion einschleusen.

Abbildung 149: Phasen und Anfangsbedingungen für den Abbau von Prometon.

Ausgehend von Prometon werden mit den beiden Reaktionstypen Hydrolyse und reduktive Dealkylierung von der Phase im Modus monomolekular" die Reaktionen erzeugt, wie sie in Abbildung 150 gezeigt sind.

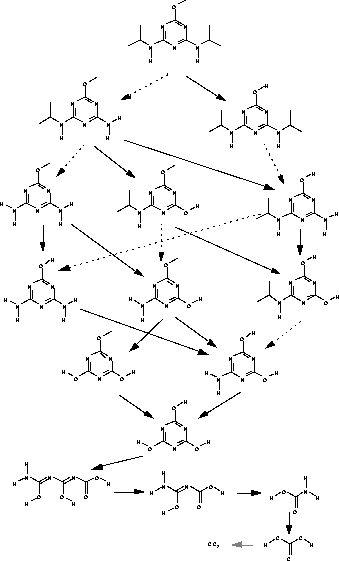
Abbildung 150: Abbau von Prometon durch reduktive Dealkylierung (gestrichelt) und Hydrolyse (durchgezogen). Die Reaktionen werden als Reaktionen pseudoerster Ordnung durchgeführt. Der formal für die Dealkylierung verwendete Wasserstoff und das Wasser für die Hydrolyse, die in großem Überschuß vorliegen, werden während der Reaktion hinzugefügt. Bei der Reduktion wird Propan abgespalten, während bei der Hydrolyse Methanol, Ammoniak und Kohlendioxid abgespalten werden können.

Unter Berücksichtigung der Geschwindigkeitskonstanten für die Reaktionen ergeben sich Konzentrationsverläufe für Prometon und seine Abbauprodukte, wie sie in Abbildung 151 gezeigt sind.

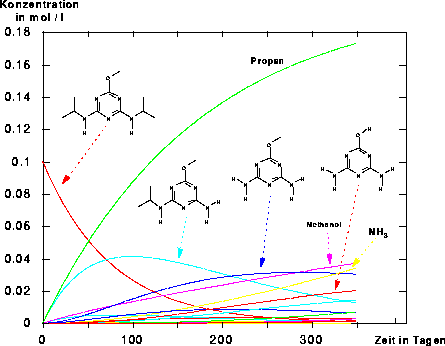
Abbildung 151: Konzentrationsverläufe für Prometon und seine Abbauprodukte.

In Abbildung 151 sind die Konzentrationsverläufe für den Abbau von Prometon angegeben. Die Reaktionszeit wurde dabei so gewählt, daß am Ende 99% des Prometons reagiert haben. Alternativ dazu wurde die Berechnung auch nur für eine Halbwertszeit (Umsatz von 50%) durchgeführt. Die Berechnungszeiten für diese beiden Umsätze und die beiden Integrationsverfahren Gear-Algorithmus (langsamstes) und Methode nach Runge-Kutta-Merson (schnellstes) sind in der nachfolgenden Tabelle zusammengefaßt. Es wurden dabei alle drei Möglichkeiten der Regeln getestet: in C++ geschriebene und gelinkte Regeln, Tcl-Regeln, die interpretiert wurden, und compilierte Tcl-Regeln.


Methode	Gear		Runge-Kutta-Merson
Umsatz	0.5	0.99	0.5	0.99
C++	1:20	6:38	0:47	1:57
Tcl compiliert	2:55	8:15	2:30	3:31
Tcl interpretiert	2:54	8:21	2:25	3:29

Tabelle 1: Berechnungszeiten auf einer SparcStation 10/50 mit 32 MB in Min.:Sek.

Es zeigt sich deutlich die höhere Geschwindigkeit der Methode nach Runge-Kutta-Merson, die bei der längeren Berechnungszeit für den Umsatz von 99% im Verhältnis noch größer ist. Schreibt man die Regeln in der Programmiersprache C++, ist die benötigte Zeit immer etwa um 1:30 Min.:Sek. kürzer. Vergleicht man schließlich die Zeiten der compilierten mit denen der interpretierten Tcl-Regeln, so kann man den erwarteten Geschwindigkeitsvorteil nicht erkennen. Es ist sogar so, daß der EROS7-Lauf mit compilierten Tcl-Regeln meist etwas länger gedauert hat. Diese kleinen Unterschiede liegen allerdings innerhalb der Genauigkeit der Zeitmessung. Alle Zeiten wurden als benötigte User- und System-Time für den Prozeß unter UNIX bestimmt. Die Abrechnung dieser Zeiten ist allerdings nicht ganz unabhängig von der Systemauslastung, weshalb es von Messung zu Messung zu Schwankungen kommt. Da beim Übergang von interpretierten zu compilierten Tcl-Regeln die flexible Anbindung und damit die Änderungsmöglichkeit verloren geht und dem kein Geschwindigkeitsgewinn gegenübersteht, kann auf die Möglichkeit, compilierte Tcl-Regeln zum System zu binden, verzichtet werden, zumal dafür ein entsprechender Compiler mit dazugehöriger Bibliothek Voraussetzung sind.

7.1.3.2. Jährliche Ausbringung von s-Triazinen

Neben der Simulation der einmaligen Ausbringung können mit EROS7 auch die Konzentrationsverläufe bei einer jährlichen Ausbringung von Prometon studiert werden. Es ist bekannt, daß es nach der Ausbringung bestimmter s-Triazinherbizide bezüglich mancher Pflanzen im darauffolgenden Jahr Unverträglichkeiten gibt. Da das Herbizid selbst nach einem Jahr zu etwa 99% abgebaut ist, dürfte diese an einem Abbauprodukt liegen, das sich noch im Boden befindet. Bei einer jährlichen Ausbringung würden sich diese Produkte im Boden anreichern. Dies läßt sich mit EROS7 vorhersagen und ist für den Zeitraum von gut drei Jahren in Abbildung 152 gezeigt.

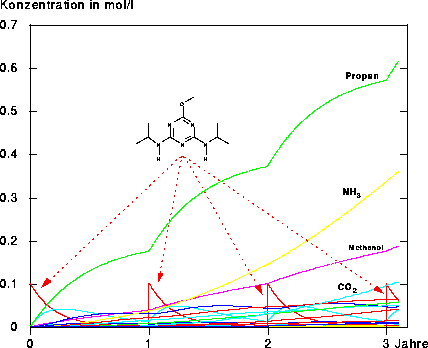
Abbildung 152: Jährliche Ausbringung der gleichen Menge Prometon.

Da man in Abbildung 152 vorwiegend die Konzentrationsverläufe der Endabbauprodukte Propan, Ammoniak, Methanol und Kohlendioxid sieht, an Zwischenprodukten jedoch wenig zu erkennen ist, wir in Abbildung 153 der Konzentrationsbereich bis 0.125 mol/l herausvergrößert.

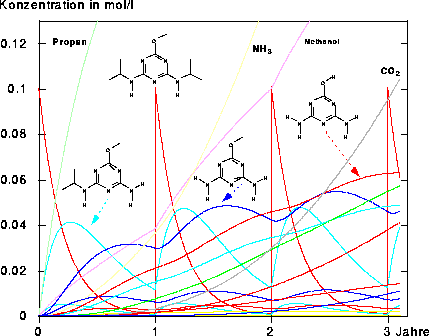
Abbildung 153: Jährliche Ausbringung der gleichen Menge Prometon. Ausschnitt für Konzentrationen bis 0.125 mol/l.

Berechnungszeit auf einer SparcStation 10/50 mit 32 MB in Min.:Sek.: 42:55 (Gear, C++)

In Abbildung 153 kann man erkennen, daß sich ein Teil der Abbauprodukte von Prometon über die Jahre hin im Boden anreichern.

Wenn Sie möchten, können Sie hier selbst ein Beispiel rechnen und die Ergebenisse anzeigen lassen.

robert(at)robert-hoellering.de